Modul 2 » Magnituden und Farbindex

Scheinbare Helligkeit und Magnituden

Zunächst werden wir uns um die scheinbare Helligkeit kümmern.

Das heutige System, mit dem wir Helligkeiten beschreiben, hat einen wahrhaftig historischen Ursprung. Es ist eine uralte "Tradition", mit Vorteilen aber auch Nachteilen: etwas ganz typisches für die Astronomie. Der griechische Astronom Ptolemäus (zirka 100 bis 170 n. Chr.) hat die Sterne des Nachthimmels in jeweils eine von sechs Helligkeits-Kategorien zugeordnet. Er gab den hellsten Sternen eine Magnitude von 1, etwas weniger hellen Sternen die Magnitude 2, und so weiter, bis zu den dunkelsten Sternen, die grade noch sichtbar waren. Letztere wurden der Magnitude 6 zugeordnet. Die Skala ging also von 1 bis 6. Auf deutsch nennen wir diese Magnituden auch Größenklassen oder einfach Größen. Eventuell hat der ebenfalls griechische Astronom Hipparchos diese sechs Magnituden-Klassen sogar schon um 120 v. Chr. verwendet, sicher überliefert ist aber nur die Arbeit von Ptolemäus.

Heute nutzen wir tatsächlich eine Weiterentwicklung dieses Systems, und sprechen auch noch von Magnituden. Allerdings ist die moderne Magnitude keine Kategorie mehr, sondern eine Größe, mit der wir stufenlos die scheinbare Helligkeit von Sternen angeben. Die Skala der Magnituden ist somit auch nicht mehr begrenzt (wie sie es bei den alten Griechen war), denn mit Teleskopen können wir inzwischen immer lichtschwächere Sterne messen.

Die moderne Definition einer Magnitude wurde so gewählt, dass sie ungefähr zu der historischen Skala von Ptolemäus passt: helle Sterne des Nachthimmels sollten eine Magnitude um 1,0 haben, während Sterne mit einer Größe von 5,0 bis 6,0 nur unter sehr dunklem Himmel und für gute Augen sichtbar sind. Es gilt also weiterhin: je größer die Magnitude, desto dunkler der Stern. Und somit kommt es, das sehr helle Objekte sogar negative Magnituden haben!

Folgende Illustration gibt einen Überblick der scheinbaren Helligkeiten einiger Himmelskörper.

Zusätzlich zu scheinbaren Magnituden sind auch einige Grenzen eingetragen, also Magnituden bei denen Sterne grade noch hell genug sind, um z.B. mit einem bestimmten Teleskop gesehen werden zu können.

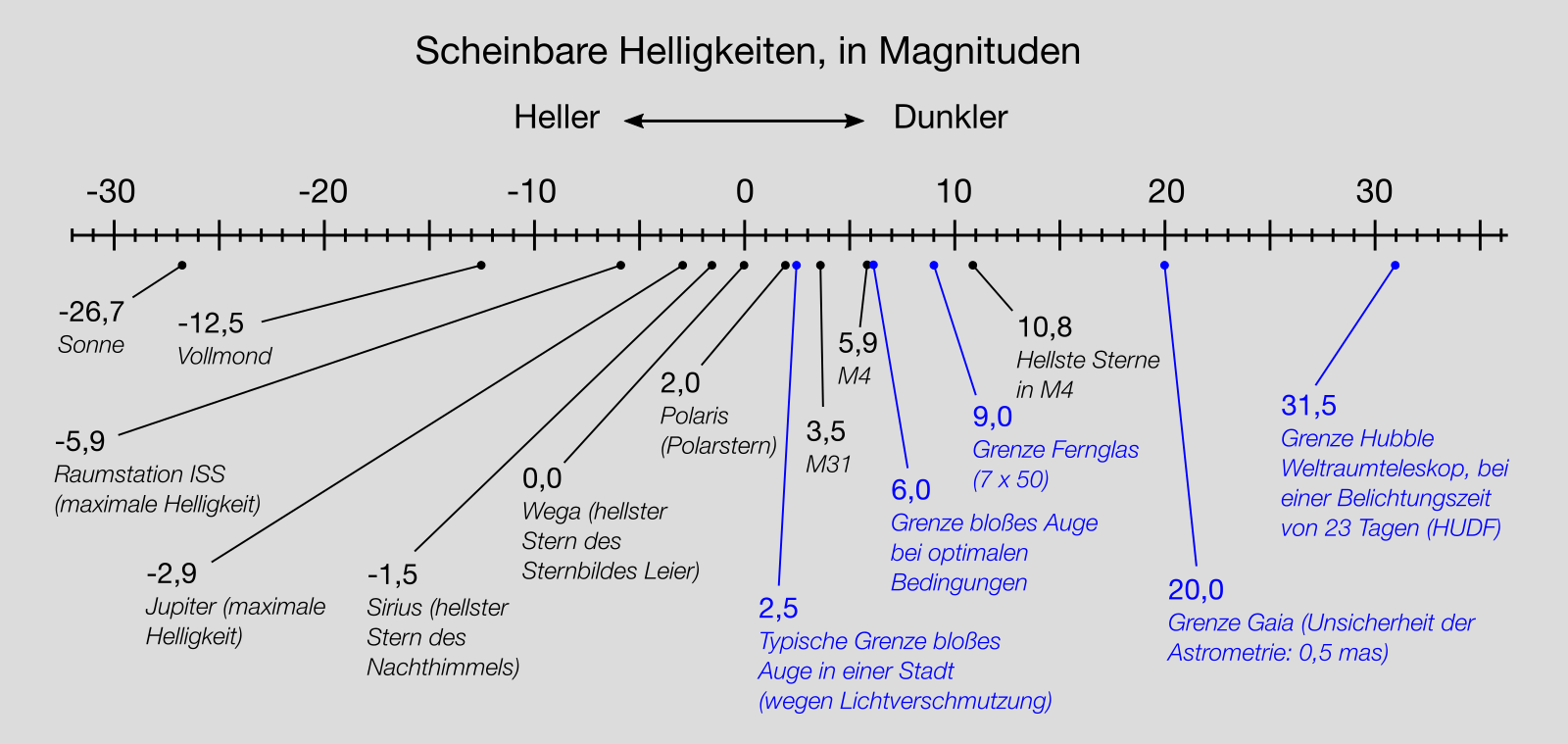
Den Kugelsternhaufen M4 kennst du ja schon aus dem ersten Modul. Für solche ausgedehnten Objekte ist hier die scheinbare Helligkeit des gesamten Objektes angegeben. Also erscheinen uns alle Sterne von M4 zusammengenommen so hell wie ein einzelner Stern der Magnitude 5,9.

Natürlich muss eine moderne Definition auch objektiv sein, und mathematisch formuliert werden können, damit wir die scheinbare Helligkeit auch messen und nicht nur abschätzen können. Magnituden sind eine Helligkeitsskala, die durch den Strahlungsfluss des einfallenden Lichtes definiert ist. Dieser Strahlungsfluss, wir nennen ihn hier $F$, entspricht der Energie des einfallenden Lichtes pro Zeiteinheit und Sammelfläche. Es ist also die "Leistung", die wir von einer bestimmten Quelle (z.B. einem Stern) mit unserem Teleskop empfangen. Und daraus ergibt sich die scheinbare Magnitude $m$ dieser Lichtquelle mit folgender Definition:

Diese Definition schauen wir uns jetzt ganz genau an.

• Zunächst einmal bemerkst du, dass Magnituden eine "logarithmische" Skala sind, also vom Logarithmus des Strahlungsflusses $F$ abhängen. Das wurde historisch so gewählt, da man dachte, dass wir mit unsere Augen Helligkeiten logarithmisch wahrnehmen. Das ist zwar aus heutiger Sicht nicht ganz korrekt, aber tatsächlich ist diese Wahl angemessener als einfach nur den Fluss zu verwenden. Denn wenn ein Objekt doppelt so viel Energie abstrahlt wie ein anderes (der Fluss also doppelt so groß ist), nehmen wir es nicht doppelt so hell wahr, sondern nur "ein wenig" heller.
• Dann ist da dieses $-2{,}5$. Das Minuszeichen bewirkt, dass der Magnitudenwert mit abnehmenden Fluss zunimmt, so wie bei Ptolemäus. Der Faktor $2{,}5$ wurde gewählt, damit diese modernen Magnituden ungefähr zu den historischen Magnituden passen.
• Und dann wunderst du dich sicherlich noch, was das $C$ in der Formel soll. Dieses $C$ ist eine Konstante. Sie hat ihren Ursprung darin, dass man sich ja irgendwie entscheiden muss, welche Helligkeit der Magnitude Null entspricht. Historisch hat man festgelegt, dass der Stern Wega eine scheinbare Magnitude von $0{,}0$ haben soll. Somit muss in der obigen Formel die Konstante angepasst werden, damit für Wega genau $m=0{,}0$ rauskommt.

Dieser letzte Punkt, zu der Konstante $C$, kommt dir vielleicht etwas unpraktisch vor. Der Fluss $F$, den wir für einen bestimmten Stern messen, hängt von unzähligen Details ab, unter anderem wir groß unser Teleskop und wie klar die Luft ist. Wir müssten $C$ also wirklich immer wieder neu bestimmen. In der Praxis ist der Umgang mit Magnituden aber glücklicherweise viel einfacher, und hier kommen die Eigenschaften der Logarithmusfunkion ins Spiel. Wenn wir die Differenz zwischen zwei Magnituden bilden (nennen wir sie $m_1$ und $m_2$, es könnten z.B. die Magnituden von zwei Sternen "1" und "2" sein), verschwindet $C$ einfach aus der Formel:

Und wenn wir uns an die Eigenschaft der Logarithmusfunktion erinnern, dass $\log_{10}(a) - \log_{10}(b) = \log_{10}(a/b)$ (falls nicht, guckst du hier), dann können wir diese Magnitudendifferenz wie folgt schreiben:

Die Differenz der scheinbaren Magnituden von zwei Objekten ergibt sich also direkt aus dem Verhältnis der zwei Strahlungsflüsse zueinander (vorausgesetzt, diese wurden unter gleichen Bedingungen gemessen)! Das bedeutet insbesondere, dass wir uns gar nicht mehr um die Einheit dieser Strahlungsflüsse kümmern müssen (oder anders gesagt, wir können diese Einheit frei Wählen), denn es geht nur noch um das Verhältnis. Wenn wir z.B. messen, dass der Fluss von einem Stern x-mal so groß ist wie der Fluss eines anderen Sterns, können wir die Differenz ihrer scheinbaren Magnituden errechnen. Und der Quotient eines Flusses und dem Fluss von Wega (dieser entspricht ja per Definition einer Magnitude 0) führt direkt zur scheinbaren Magnitude.

Die Technik hinter Helligkeitsmessungen

Wir beschäftigen uns nun kurz damit, wie der Strahlungsfluss eines Sterns in der modernen Astronomie gemessen wird.

Als erstes brauchen wir dazu ein Teleskop, um möglichst viel Licht des Sterns zu "sammeln". Das Teleskop agiert dabei im wesentlichen genau wie eine konvexe Linse (auch Sammellinse genannt), so wie du sie auch in einer Lupe findest. Das einfallende Licht wird fokussiert, und es entsteht in der Fokalebene ein reelles Abbild des Himmelsausschnits auf den das Teleskop gerichtet ist. In diese Fokalebene könnte man ein Stück weißes Papier als Schirm halten, und würde darauf die verschiedenen Sterne als kleine helle Punkte sehen.

Und an dieser Stelle, statt des Papierstücks, kommt nun ein "Instrument" ins Spiel. Als Instrument bezeichnen wir in der beobachtenden Astronomie die Geräte und Sensoren, mit denen das Licht tatsächlich gemessen wird. Um scheinbare Helligkeiten zu messen werden heutzutage fast ausnahmslos sogenannten CCD-Kameras genutzt, und das sowohl in Sternwarten wie auch bei Weltraumteleskopen. CCDs sind lichtempfindliche Sensoren mit vielen Pixeln, ganz ähnlich zu den Sensoren in einer Smartphone-Kamera. Die in der Astronomie verwendeten CCD-Kameras sind extrem empfindlich: sie sind tatsächlich praktisch dazu in der Lage, nach der Belichtung zu zählen, wieviele Photonen auf jedes einzelne Pixel gefallen sind. Allerdings können sie die Photonen dabei nicht nach Wellenlänge unterscheiden. Die CCD liefert also nur ein Bild der Helligkeit, ohne Information zum Spektrum oder wenigstens der Farbe des Lichtes.

Fassen wir zusammen: mit der Kombination Teleskop und CCD-Kamera bekommen wir ein digitales Bild des Himmels, das uns sagt, wieviele Photonen in jedes Pixel dieses Bildes gefallen sind. Diese Anzahl nennt man dann auch den "Wert" des Pixels.

Das Bild von einem Stern erstreckt sich im Regelfall als eine kleine Scheibe über mehrere benachbarte Pixel. Wir können aber einfach die Werte dieser Pixel addieren um zu errechnen, wie viele Photonen wir von einem Stern während der gewählten Belichtungszeit empfangen haben 1. Und diese Zahl können wir direkt als Fluss $F$ des Sterns verwenden, um seine Helligkeit wie oben beschrieben in Magnituden auszudrücken.

Farben, Filter und Farbindex

CCD-Sensoren liefern uns wie eben besprochen keine Farbinformation. Aber wie können wir dann denn überhaupt ein Farbbild aufnehmen? Und wie können wir die Farbe eines Sterns messen und beschreiben? Die Antwort liegt in der Verwendung von Filtern, die in der Regel zwischen Teleskop und CCD-Sensor platziert werden.

Ein Filter sieht aus wie eine farbig getönte oder verspiegelte Glasscheibe, und das ist er im Prinzip auch. Er selektiert die einfallende Strahlung nach der Wellenlänge, und lässt also nur Photonen in bestimmten Wellenlängenbereichen durch. Es gibt unzählige verschiedene Filter, und wir werden uns hier nur mit den einfachsten Farbfiltern beschäftigen. Wenn zum Beispiel ein Filter nur Photonen zwischen 600 und 900 nm durchlässt, würden wir ihn als "rot" bezeichnen, da grüne und blaue Photonen von diesem Filter entweder absorbiert oder reflektiert, aber nicht durchgelassen werden.

Bildquelle: M. de la Nougerede, UCL/MSSL

Fotografiert man ein astronomisches Objekt nun mit einer CCD-Kamera und verschiedenen Filtern, könnte man daraus ein Farbbild erstellen.

Man kann aber auch einfach direkt die Helligkeiten der Sterne in den verschiedenen Filtern messen, ganz ohne Farbbild. Und genau so wird es in den allermeisten wissenschaftlichen Beobachtungen gemacht. Scheinbare Magnituden werden also immer in einem bestimmten Filter angegeben, und je nach Filter hat ein Stern unterschiedliche Magnituden.