Modul 3 » Bestimmung des Alters eines Kugelsternhaufens

Wir haben nun die FHDs für zwei Sternhaufen M4 und M92 erstellt und konnten daraus die Entfernung von M92 bestimmen. Aus einem FHD lassen sich jedoch noch weitere interessante Größen ableiten, wie beispielsweise das Alter eines Sternhaufens.

Aus Modul 2 weißt du schon, dass Sterne die meiste Zeit ihres Lebens auf der Hauptreihe verbringen, die sich von den roten und leuchtschwachen Sternen hin zu den blauen und leuchtkräftigen Sternen erstreckt. Dabei bestimmt die Masse eines Sterns, wo sich dieser im FHD auf der Hauptreihe befindet und wie dessen Entwicklung aussieht.

Wir haben auch gesehen, dass die Hauptreihe in einem FHD bei einer bestimmten Masse abknickt und nur noch Sterne mit geringerer Masse vorhanden sind. Im Zuge des Ende eines Sterns, wandert dieser von der Hauptreihe aus zunächst auf den Riesenast des FHD und ein Teil der Sterne von dort aus schließlich auf den Horizontalast.

Was sind Isochrone?

Diese Entwicklung der Sterne kann man sehr gut anhand der FHD von Sternhaufen verfolgen. Je nachdem wie weit der Abknickpunkt der Hauptreihe und der Riesenast vorangeschritten sind, lässt sich dabei auch das Alter des Sternhaufens bestimmen. Dazu simuliert man die Entwicklung eines Sternhaufens mit numerischen Methoden bis zu einem bestimmten Alter. Daraus erhält man eine theoretisch erwartete Verteilung der Sterne im FHD, die den für das Alter charakteristischen Abknickpunkt der Hauptreihe und die Entwicklung des Riesenasts zeigt. Diese resultierende Sternenverteilung wird Isochrone genannt (griech. iso = gleich, chronos = Zeit).

Berechnet man nun eine Vielzahl dieser Isochronen und vergleicht diese mit dem FHD eines beobachteten Sternhaufens, so kann man dessen ungefähres Alter bestimmen, indem man die Isochrone auswählt, die sich am besten mit dem FHD überdeckt.

Die zwei Isochrone für unterschiedliche Alter eines Sternhaufens zeigen den Abknickpunkt der Hauptreihe in Abhängigkeit des Alters und die Entwicklung des Riesenasts.

Absolute Helligkeit

Bisher haben wir uns bei der Erstellung der FHDs auf die scheinbare Helligkeit der Sterne beschränkt. Die scheinbare Helligkeit allein gibt allerdings keine Aussage über die tatsächliche Leuchtkraft eines Sterns. Die Sonne hat wegen ihrer Nähe zur Erde eine sehr große scheinbare Helligkeit, während ein ähnlicher Stern in großer Entfernung eine viel geringere scheinbare Helligkeit besitzt. Um die Helligkeiten aller Sterne sinnvoll miteinander vergleichen zu können, muss man also deren Entfernungen kennen. Entfernung und scheinbare Helligkeit führen schließlich zur absoluten Helligkeit.

Diese ist definiert als die scheinbare Helligkeit, die ein Stern in einer Entfernung von 10pc hätte. Man kann sich das so vorstellen, als würde man einen Stern auf die Entfernung von 10pc verschieben und dann dessen scheinbare Helligkeit messen. Macht man dies mit allen Sternen deren Entfernung bekannt ist, kann man also deren Helligkeiten miteinander vergleichen, da diese dann auf dieselbe Entfernung von 10pc normiert wurden.

Die Beziehung zwischen absoluter Helligkeit MM, scheinbarer Helligkeit mm und der Entfernung DD eines Sterns nennt man das Entfernungsmodul:

m−M=5log⁡10(D10pc)=5log⁡10(D[pc])−5m - M = 5\log_{10}\left(\frac{D}{10\textrm{pc}}\right) = 5\log_{10}\left(D [\textrm{pc}]\right) - 5

Hier sind zwei Dateien aufgelistet, in denen Daten von insgesamt zehn simulierten Isochronen stehen. In sim_alter.tsv steht das jeweilige Alter, bis zu dem die Isochrone simuliert wurde und in sim_magnituden.tsv sind wie bei den vorherigen FHD die Helligkeiten der Sterne im blauen und roten Farbbereich angegeben, aus denen man beim Plotten den Farbindex berechnen muss.

Nun möchten wir die Isochronen mitsamt dem FHD von M4 in einem Plot darstellen. Erstelle eine neue Datei alter_M4.py und plotte zunächst wie schon in fhd_M4_M92.py das FHD von M4. Allerdings soll jetzt auf der y-Achse nicht mehr die scheinbare, sondern die absolute Helligkeit aufgetragen werden. Berechne dafür zunächst das Entfernungsmodul mit deinem Ergebnis für die Entfernung von M4. Mit der scheinbaren Helligkeit aus den Daten und dem Entfernungsmodul kannst du dann also die absolute Helligkeit berechnen - berücksichtige dabei wieder die Extinktion.

Zusätzlich müssen wir auch die beiden Dateien sim_alter.tsv und sim_magnituden.tsv laden, wie wir es auch schon mit katalog_M4.tsv gemacht haben. Insgesamt haben wir jetzt zehn Isochronen zu plotten. Wenn Du einen Blick in die Datei sim_magnituden.tsv wirfst, siehst Du, dass die Spalten mit R_0 B_0 R_1 B_1 usw. benannt sind. Anstatt alle Isochronen in mühsamer Copy-Paste Arbeit zu plotten, gibt es dazu eine elegantere Möglichkeit, die sich for-Schleife nennt.

Die folgende for-Schleife gibt dir beispielsweise die Fakultät einer beliebigen ganzen Zahl n aus:

fakultaet=1
n=7
for i in range(1,n):
    fakultaet*=i
print(fakultaet)

In diesem Fall können wir i von 0 bis 9 laufen lassen, da es hier zehn Isochronen nummeriert von 0 bis 9 gibt. Zuerst ruft man also die Spalten R_0 und B_0, danach R_1 und B_1 usw. auf, um damit die Isochronen zu plotten. Statt also zehn Mal dieselben drei Zeilen für die verschiedenen Isochronen hintereinander zu schreiben, haben wir mit der for-Schleife das Problem auf nur einmal drei Zeilen reduziert.

Wir können die Isochronen also elegant in einer einzigen for-Schleife plotten, indem wir mit der Iterationsvariablen i immer die Spalte R_i bzw. B_i aufrufen, was in python durch sim_magnituden["R_"+str(i)] bzw. sim_magnituden["B_"+str(i)] geschieht. In plt.plot() plotten wir wie gewohnt die Helligkeit gegen den Farbindex und benennen die jeweilige Isochrone mit dem entsprechenden Eintrag aus sim_alter.tsv.

import numpy as np
import matplotlib.pyplot as plt

# Als erstes laden wir wie üblich den Katalog von M4:
katalog = np.genfromtxt("katalog_M4.tsv", delimiter="\t", names=True)

# Die Korrektur der Extinktion von M4:
A_R_M4 = 0.85
A_B_M4 = 1.49

D_M4 = ... #Trage deinen Wert für die Entfernung von M4 ein (Einheit: pc)
# Und das Entfernungsmodul von M4:
EntMod = ... #Berechne hier das Entfernungsmodul mit der gegebenen Formel

# Und erstellen das FHD
plt.plot(
    (katalog["phot_bp_mean_mag"] - A_B_M4) - (katalog["phot_rp_mean_mag"] - A_R_M4),
    ..., #Hier kommt die absolute Helligkeit rein (Berücksichtige die Extinktion)
    label="M4",
    marker=".", markersize=2, linestyle="None", alpha=0.3, rasterized=True
    )

# Jetzt laden wir die Ergebnisse der Sternentwicklungssimulation
sim_alter = np.genfromtxt("sim_alter.tsv", delimiter="\t", names=True)
# (Probier doch mal ein print(sim_alter) um die Liste zu sehen)
sim_magnituden = np.genfromtxt("sim_magnituden.tsv", delimiter="\t", names=True)

#Die Isochronen werden in der for-Schleife nacheinander geplottet, i läuft dabei von 0 bis 9
for i in range(10):
    sim_R = sim_magnituden["R_"+str(i)]
    sim_B = sim_magnituden["B_"+str(i)]
    plt.plot(sim_B - sim_R, sim_R, label="{:.2f} Gyr".format(sim_alter["ages"][i]))

plt.gca().invert_yaxis()
plt.title("Altersbestimmung von M4")
plt.xlabel("Farbe B - R [mag]")
plt.ylabel("Absolute Helligkeit M [mag]")
plt.legend()

plt.tight_layout()
plt.show()

Mit dem oben beschriebenen Code sollte der Plot der Isochronen etwa so aussehen:

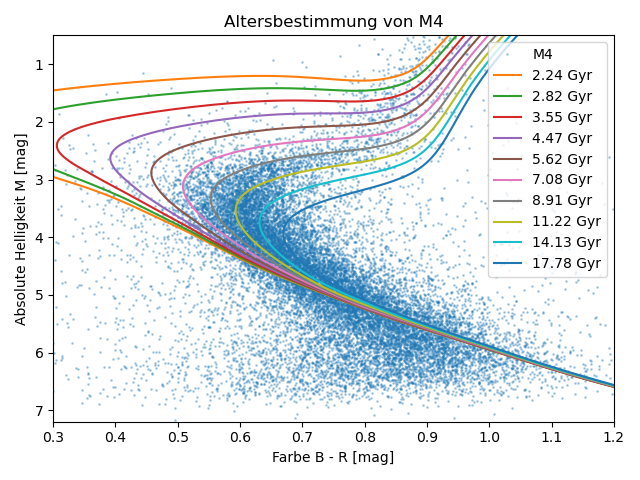
Mit dem Einstellen der Grenzen des Plots oder der Zoom-Funktion kannst Du dir die einzelnen Isochronen genauer anschauen. Nun kannst Du entscheiden, welche der zehn Isochronen am besten das FHD von M4 darstellt. Das Alter dieser Isochrone ist dann auch das ungefähre Alter des Sternhaufens M4.

Du hast nun das Alter eines Kugelsternhaufens bestimmt. Dasselbe könntest du auch mit M92 ausprobieren, die Vorgehensweise ist dabei dieselbe.

Zusätzlich kannst Du noch die Unsicherheit des Verhältnisses der Entfernungen von M92 und M4 berechnen

Bestimmung der Unsicherheit von DM92DM4\frac{D_{\textrm{M92}}}{D_{\textrm{M4}}}

oder sofort mit Modul 4 weitermachen:

Weiter mit Modul 4.

Letzte Aktualisierung: 2022-11-23 11:57