Modul 3 » Farben-Helligkeits-Diagramme von M4 & M92, Extinktion

Du hast jetzt die Datensätze von M4 & M92 in Dateien abgespeichert. Diese kannst du nun mit Python einlesen, und die Farben-Helligkeits-Diagramme zu ersetllen. Dazu kannst du deinen eigenen Code schreiben, oder dich an diesem vorgefertigten Skript orientieren (speichere ihn z.B. als fhd_M4_M92.py):

import numpy as np
import matplotlib.pyplot as plt

# Als erstes laden wir die Kataloge von M4 und M92:
katM4 = np.genfromtxt("katalog_M4.tsv", delimiter="\t", names=True)
#katM4 = np.delete(katalog, 0) # Entfernen der nan-Zeile (Aladin Striche unter Namen)
katM92 = np.genfromtxt("katalog_M92.tsv", delimiter="\t", names=True)

# Zur Erinnerung: so könntest die Namen der Spalten nachsehen:
print("Namen der Spalten:", katM4.dtype.names)

# Jetzt rufen wir einfach zweimal hintereinander die Funktion "plt.plot()" auf.
# Einmal mit M4, und dann einmal mit M92:
plt.plot(
    katM4["phot_bp_mean_mag"] - katM4["phot_rp_mean_mag"], # Farbe: B - R
    katM4["phot_rp_mean_mag"], # Scheinbare Helligkeit: R
    label="M4",
    marker=".", markersize=2, linestyle="None", alpha=0.3, rasterized=True
    )
plt.plot(
    katM92["phot_bp_mean_mag"] - katM92["phot_rp_mean_mag"],
    katM92["phot_rp_mean_mag"],
    label="M92",
    marker=".", markersize=2, linestyle="None", alpha=0.3, rasterized=True
    )

# Wie schon im Modul 2 gemacht ändern wir die Richtung der y-Achse:
plt.gca().invert_yaxis()

# Und Beschriften das Diagram:
plt.title("Gaia-FHDs von M4 und M92")
plt.xlabel("Farbe B - R [mag]")
plt.ylabel("Scheinbare Helligkeit R [mag]")
plt.legend()

# Optional: setzte folgende Zeile direkt vor show() oder savefig(),
# dann wird der Abstand zwischen Beschrifung und Diagram optimiert:
plt.tight_layout()

# Und zum Schluss eines von
plt.show()
#plt.savefig("M4_M92_FHDs.png", dpi=300)

Du entdeckst in diesem Skript ein paar neue Elemente, die wir kurz kommentieren:

Wir haben die Option label="Mein Label" zu den beiden Aufrufen von plt.plot() hinzugefügt, und somit den beiden Datensätzen "labels" (also Namen) gegeben. Weiter unten im Skript rufen wir plt.legend() auf, und bewirken damit, dass ganz automatisch eine kleine Legende (beschriftet mit unseren labels) angezeigt wird.
Wir haben auch noch die Option alpha=0.3 in den plt.plot() genutzt, die die Punkte leicht durchsichtig macht. Damit lässt sich die Verteilung der Punkte besser wahrnehmen.

Wir nehmen hier an, dass du den Skript von dem Ordner aus ausführst, in dem auch die beiden TSV-Dateien sind. Sonst würde Python die TSV-Dateien nicht finden. Alternativ kannst du natürlich auch Pfade (statt nur Dateinamen) für die TSV-Dateien angeben.

Lass den Skript nun laufen. Der resultierende Plot sollte in etwas so aussehen:

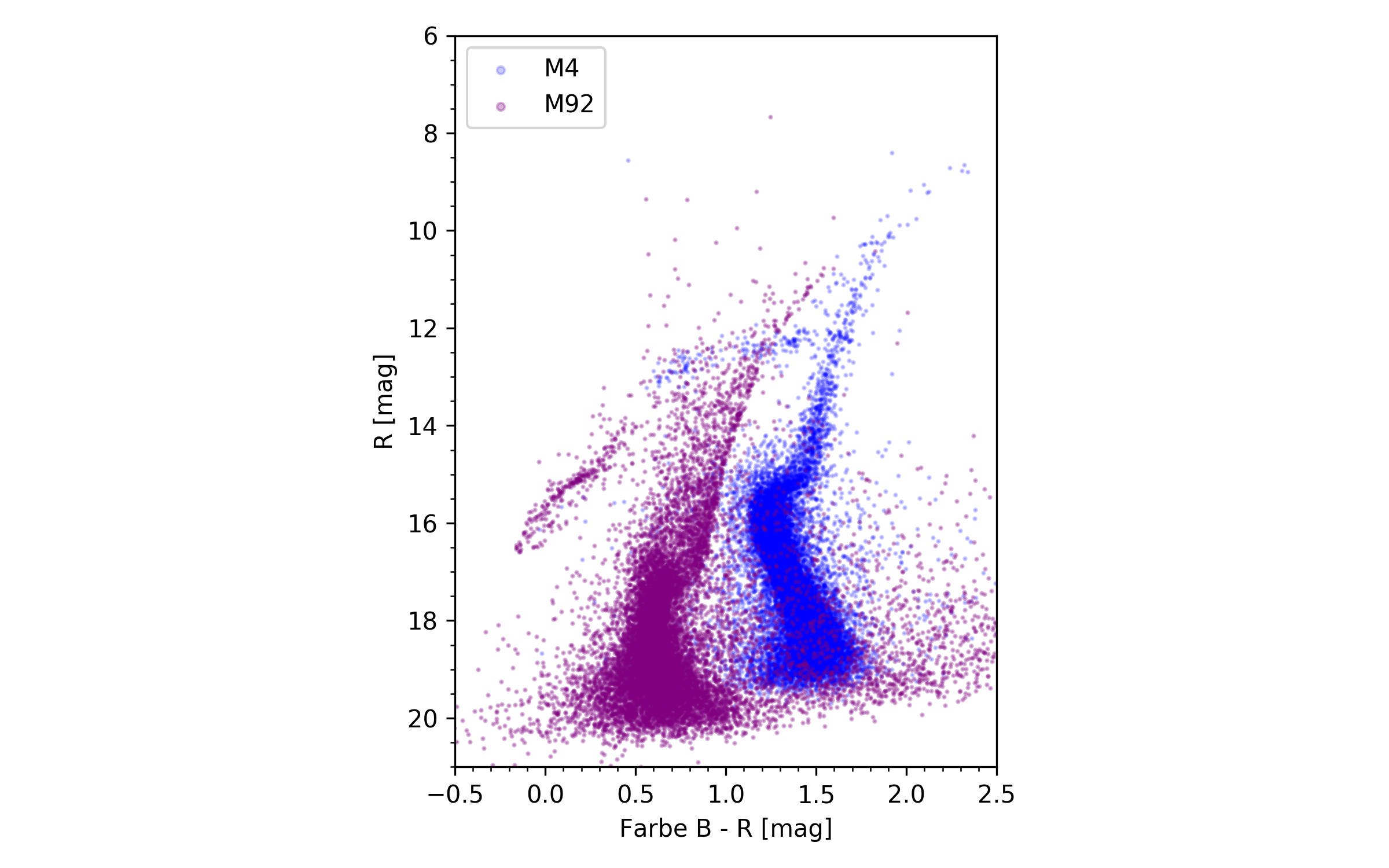
Du siehst, dass der Horizontalast von M92 bei größeren Magnituden liegt, als der von M4. Das war auch zu erwarten, M92 ist schließlich weiter von uns entfernt als M4. Größere Magnituden bedeuten eine kleinere Helligkeit, und wir gehen davon aus, dass Sterne im Horizontalast immer die gleiche Leuchtkraft besitzen.

Was du auch erkennen kannst ist, dass die FHDs von M4 und M92 in Richtung der Farbe (also entlang der x-Achse) verschoben sind.

Das lässt sich durch die sogenannte Extinktion $A$ erklären. Zwischen uns und den Kugelsternhaufen liegt Staub. Dieser interagiert mit dem Licht, er streut es zum Beispiel. Verschiedenen Wellenlängen sind dabei unterschiedlich stark betroffen. Kurze Wellenlängen, also blaueres Licht, wird stärker gestreut als rotes. Da wir als Farbe die Helligkeit in zwei Filtern, also bei zwei verschiedenen Wellenlängebereichen nehmen, ändert sich die Farbe der Sterne, je mehr Staub in der Sichtlinie zu ihnen liegt. Diesen Effekt müssen wir korrigieren, bevor wir die Entfernung zu M92 bestimmen können!

Schon anhand der Bilder von M4 und M92 kannst du erahnen, dass zwischen uns und M4 mehr Staub liegt als zwischen uns und M92. M4 liegt tatsächlich näher an der Scheibe unserer Milchstraße, und in dem erwähnten Bild sind die Staubwolken ja sogar zu sehen. Die Extinktion ist hier erheblich. Dagegen können wir die Extinktion von M92 getrost vernachlässigen. Somit müssen wir nur die Messungen von M4 korrigieren.

Unter Anahme einer gewissen Art des Staubes kann die Farbabhängigkeit der Extinktion durch folgende Gleichung beschrieben werden 1 :

A_\text{R}\approx 0{,}567\cdot A_\text{B}

Die Gleichung beschreibt also nur einen Zusammenhang zwischen den Extinktionen in beiden Gaia-Filtern. Oder anders gesagt: sie gibt an, wieviel stärker die Extinktion in B als in R ist. Diese Gleichung sagt uns aber nicht, wie hoch die Extinktion in diesen Filtern ist! Denn das hängt davon ab, wieviel Staub sich nun zwischen uns und dem Objekt befindet.

Aus dem Vergleich der FHDs von M4 und M92 können wir aber abschätzen, das M4 ungefähr 0,64 mag "röter" ist als M92. Überprüfe diesen Wert mit deinem Plot der FHDs, und nutze dafür z.B. den Berührungspunkt zwischen Horizontalast und Riesenast der FHDs. Wie schon erwähnt nehmen wir an, dass M92 nicht von Extinktion betroffen ist.

Diese "Rötung" liegt nur an der unterschiedlichen Extinktion in den zwei Filtern! Mathematisch können wir für M4 also schreiben:

A_\text{B}-A_\text{R}\approx 0{,}64\,\text{mag}

Nun kannst du diese zwei Gleichungen kombinieren, und damit die Werte der Extinktion für M4 in beiden Filtern errechnen ( $A_\text{R}$ und $A_\text{B}$ ).

Unser FHD von M4 ist also durch diese Extionktion gestört. Wir wollen es jetzt korrigieren, damit dieses FHD so aussieht, als ob gar kein Staub vor M4 liegen würde.

Mache dazu folgendes:

Definiere in deinem Skript, oberhalb der beiden plt.plot(), die Extinktion in R und B:

A_R_M4 = 0.85 # Ist das richtig?
A_B_M4 = 1.49

Korrigiere nun das FHD von M4, indem du sämtliche Magnituden von M4 im plt.plot() um A_R_M4 und A_B_M4 verschiebst. Kleiner Tipp: durch Extinktion werden Sterne dunkler (und deren Magnituden also größer). Wir wollen mit unserer Korrektur die gemessenen Magnituden also wieder kleiner machen.

Führe den Skript nochmal aus. Wenn alles geklappt hat, sollte das FHD von M4 nun bei der selben Farbe wie das FHD von M92 liegen.

Nachdem du das FHD von M4 nun von Extinktion befreit hast, können wir uns dem nächsten Unterschied zwischen M4 und M92 widmen.

Weiter geht's zur Entfernungsbestimmung von M92

Referenzen

1.: ^ Reddening law for M4: https://arxiv.org/abs/1204.5719

Letzte Aktualisierung: 2025-06-30 23:39