Modul 3 » Leuchtkraft, Fluss & Entfernung

In Modul 2 hast du schon den Fluss $F$ kennengelernt. Der Fluss ist die Leistung, die von dem Objekt, das wir beobachten (z.B. ein Stern), auf der Sammelfläche von unserem Teleskop ankommt. Die Einheit des Flusses ist also $W\,m^{-2}$ , wobei Watt Energie pro Sekunde ist.

Wie verändert sich nun der Strahlungsfluss von einem Stern, wenn wir näher an ihm dran oder weiter von ihm weg sind? Um das genauer zu untersuchen, hilft uns eine Skizze sehr:

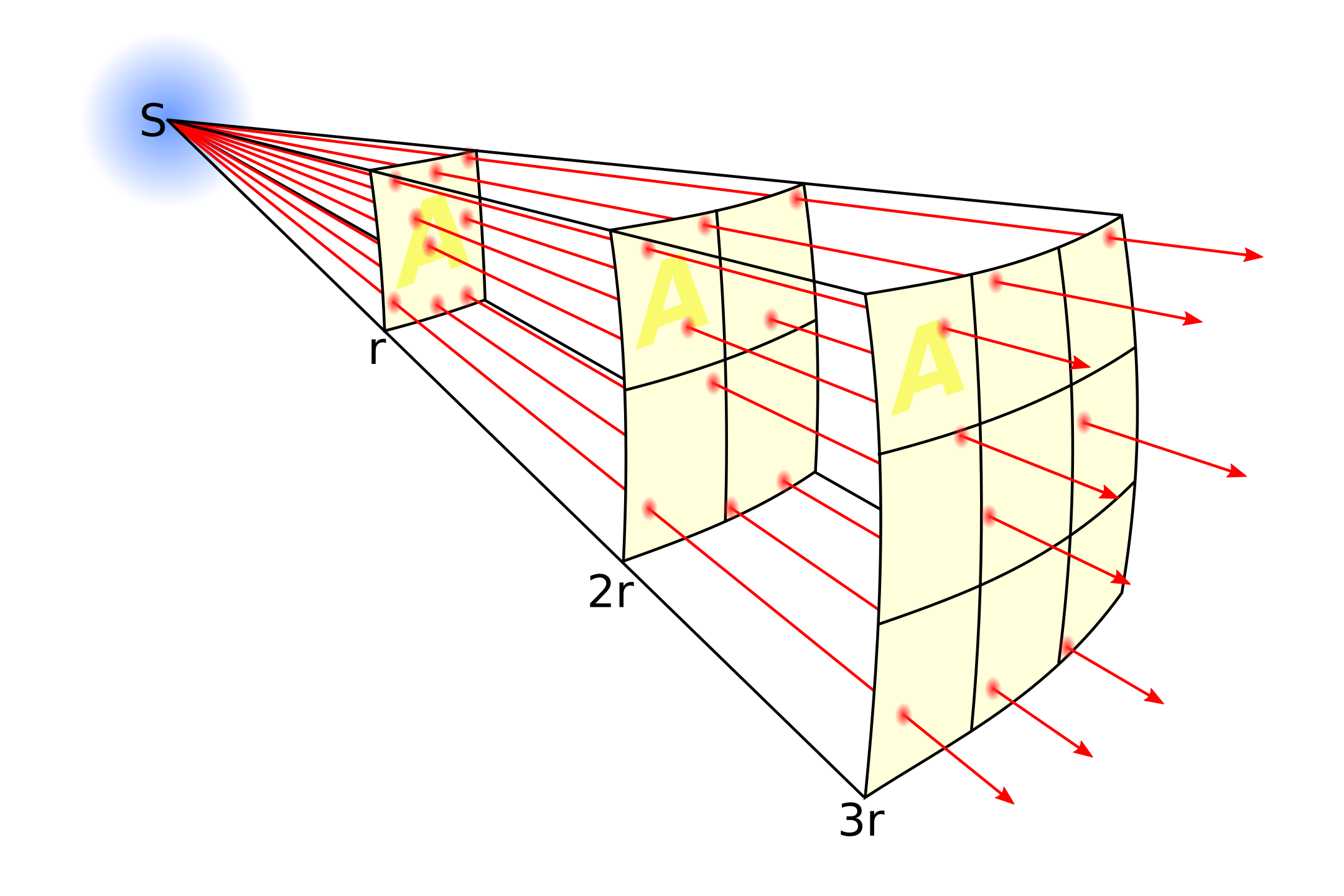
Die Veränderung des Strahlungsflusses mit dem Abstand zum Stern

Hier siehst du eine Strahlungsquelle $S$ , die Licht abstrahlt. Das ist dargestellt mit den roten Pfeilen, die von der Quelle ausgehen. Im Abstand $r$ , laufen die Lichtstrahlen durch die Fläche $A$ . Wenn wir jetzt den Abstand verdoppeln, also den Stern im Abstand $2r$ , beobachten, laufen die gleichen Lichtstrahlen durch die vierfache Fläche $4A$ . Und im dreifachen Abstand $3r$ brachen wir schon die neunfache Fläche $9A$ , um alle ausgesendeten Lichtstrahlen einzufangen!

Wie sehen also, dass es sich um einen quadratischen Zusammenhang handelt: Verdoppeln wir unseren Abstand $D$ zu einem Stern, kommt nur noch ein Viertel des Flusses an! Mathematisch kann man schreiben:

\frac{F_1}{F_2}=\frac{D_2^2}{D_1^2}

Und die Leuchtkraft?

Diese Relation können wir benutzen, um die Entfernung, Fluss und Leuchtkraft eines Sterns zu verbinden. Die Leuchtkraft $L$ ist dabei einfach die gesamte Leistung, die ein Stern in alle Richtungen abstrahlt. Sie ist also unabhängig von der Entfernung zum Stern, anders als der Fluss. Die entsprechende SI-Einheit ist deshalb einfach $W$ . In der Astronomie werden Leuchtkräfte aber meistens in der Einheit von Sonnenleuchtkräften $L_\odot$ angegeben, weil das anschaulicher ist. So weiß man direkt, wie hell ein Stern im Vergleich zu unserer Sonne ist, die übrigens auch ein "durchschnittlicher" Stern ist.

Um die Leuchtkraft eines Sterns jetzt mit dem Abstand zu diesem und dem beobachteten Fluss zu verknüpfen müssen wir eine Annahme machen; dass der Stern in alle Richtungen gleichmäßig abstrahlt. Diese Annahme ist zum Glück gut erfüllt, denn Sterne sind in sehr guter Näherung Kugeln und ihre Oberfläche ist überall etwa gleich heiß. Deshalb strahlen sie als schwarze Körper in alle Richtungen gleichmäßig ab. Mit dieser Annahme sehen wir, dass sich die vom Stern abgestrahlte Energie einfach auf der Oberfläche einer Kugel, in deren Mitte der Stern sitzt verteilt. Der Radius der Kugel ist dabei der Abstand $D$ vom Beobachter zum Stern. Ein Beobachter irgendwo auf dieser Kugeloberfläche misst dann den Fluss:

F=\frac{L}{A_\mathrm{Kugel}}

Die Formel für die Oberfläche einer Kugel mit Radius $r$ hast du vielleicht schon einmal gesehen, sie ist gegeben durch:

A=4\pi r^2

Wenn wir als Radius die Distanz $D$ vom Beobachter zum Stern einsetzen erhalten wir für den Fluss:

F=\frac{L}{4\pi D^2}

Weiter geht's hier

Letzte Aktualisierung: 2023-12-04 14:49