Modul 2 » Schwarze Körper und das Plancksche Strahlungsspektrum

Wir haben am Ende der vorherigen Seite erwähnt, dass das Spektrum der Sonne (und auch von allen anderen gewöhnlichen Sternen) sehr nahe dem Spektrum eines "Schwarzen Körpers" ist. Aber was ist das?

Jedes Objekt mit einer Temperatur über dem absoluten Nullpunkt (0 Kelvin, geschrieben 0 K, entspricht exakt -273,15 °C) sendet Strahlung über weite Bereiche des elektromagnetischen Spektrums aus. Der Ursprung dieser Strahlung liegt in den winzig kleinen zufälligen Bewegungen der Atome und Moleküle des Objekts. Diese Bewegungen sind bei warmen Objekten stärker als bei kälteren Objekten: sie machen die Temperatur eines Objektes aus. Daher nennt man die sich daraus ergebende elektromagnetische Strahlung auch thermische Strahlung.

Die Menge und die Verteilung (also das Spektrum) dieser thermischen Strahlung hängt dabei ausschließlich von der Temperatur des Objektes ab. So unterscheidet sich beispielsweise die thermische Strahlung deiner Hand nicht von der eines Stück Eisens bei der gleichen Oberflächentemperatur von 36 °C: nur diese Temperatur zählt, die chemische Zusammensetzung oder die Beschaffenheit der Oberfläche des Objektes sind dagegen irrelevant.

Die Bezeichnung Schwarzer Körper beschreibt nun ein theoretisches und idealisiertes Objekt, dass keinerlei Strahlung reflektiert. Stattdessen absorbiert (also schluckt) es sämtliche einfallende elektromagnetische Strahlung (daher der Begriff "schwarz"). Und es emittiert, strahlt also selber aus. Strahlung, die wir von so einem Schwarzen Körper empfangen würden, wäre ausschließlich thermische Strahlung. Daher sind die Begriffe thermische Strahlung und Schwarzkörperstrahlung Synonyme. In unserem Alltag gibt es keine perfekten Schwarzen Körper: selbst wenn wir ein stück schwarzes Papier betrachten empfangen wir immer noch viele Photonen die von dem Papier reflektiert wurden. So sieht das Papier je nach Beleuchtung auch unterschiedlich aus. Bei einem echten Schwarzem Körper wäre das nicht der Fall: wir würden nur thermische Strahlung von diesem Körper empfangen, und alleine die Oberflächentemperatur des Körpers würde daher seine Farbe bestimmen. Und so ist es auch mit Sternen, die fast wie echte Schwarzer Körper strahlen.

Schauen wir uns nun diese Schwarzkörperstrahlung genauer an. Wie schon erwähnt verteilt sich diese Strahlung über das elektromagnetische Spektrum. Im Jahre 1900 hat der Physiker Max Planck eine genaue mathematische Beschreibung dieses Spektrums der Schwarzkörperstrahlung hergeleitet, daher nennt man dieses Spektrum auch das plancksche Strahlungsgesetz.

Folgendes Bild zeigt dieses theoretische Spektrum, für drei verschiedene Temperaturen. Der rechte Teil ist nur ein vergrößerter Ausschnitt.

Der sichtbare Bereich des Spektrums ist durch den Regenbogen dargestellt. Bildquelle: ESA / AOES Medialab

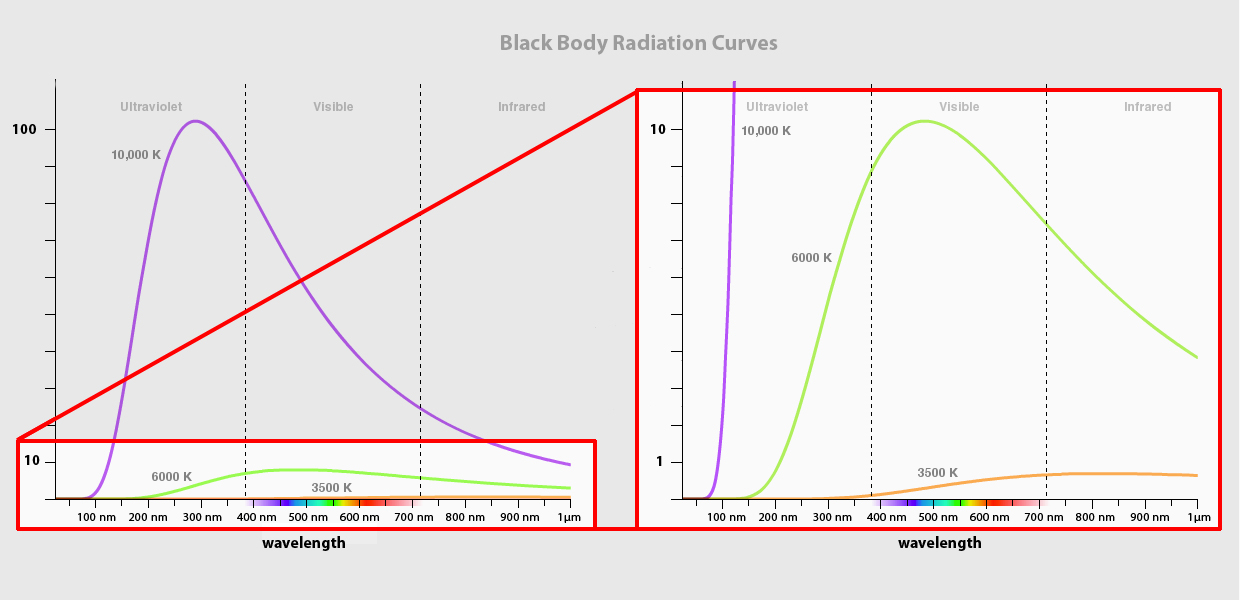
Die violette Kurve zeigt das Spektrum eines Schwarzen Körpers bei 10000 Kelvin, die flachere grüne Kurve bei 6000 Kelvin, und die nochmals flachere orangene Kurve bei 3500 Kelvin. Das deckt sich sicherlich mit deinen Erwartungen: je heißer ein Objekt ist, desto mehr Strahlung gibt es ab. Und wie wir sehen ist der Unterschied zwischen diesen Temperaturen erheblich.

Es gibt auch immer eine Wellenlänge, bei der diese Strahlung am intensivsten ist. Bei der violetten Kurve liegt diese Wellenlänge im UV-Bereich (den wir gar nicht sehen können), bei der grünen Kurve dagegen im sichtbaren Licht, um die 500 nm. Die Wellenlänge des Maximums verschiebt sich also mit der Temperatur: das Spektrum ändert sich, und damit verändert sich natürlich auch die Farbe, die wir Anhand des sichtbaren Teils des Spektrums wahrnehmen. So strahlt ein Körper bei 1000 K rötlich und bei 6000 K weißlich. Ein Objekt bei 300 K (also Raumtemperatur) strahlt hauptsächlich im Infraroten, und kaum im sichtbaren Licht. Wir sehen ihn daher nicht strahlen (sprich glühen).

Welche stellen sind am heißesten? Bildquelle: Wikimedia user Ekrem Canli

Und Sterne?

Körper mit Temperaturen über 6000 K glühen tatsächlich auch bläulich. Diese sind im Alltag vielleicht selten, allerdings nicht am Sternenhimmel! Und jetzt kennst du auch den Grund. Die Oberflächentemperatur bestimmt die Farbe eines Sterns: kühlere Sterne sind rötlicher, heiße Sterne sind bläulicher.

Es gibt eine nützliche Formel, mit der man die Wellenlänge des Strahlungsmaximums eines schwarzen Körpers einfach berechnen kann. Das ist das Wiensche Verschiebungsgesetz:

$\lambda_{\textrm{max}} [\mu \textrm{m}] = \frac{2897{,}8}{T\,[\textrm{K}]}$

Wie schon im ersten Modul erwähnt bedeutet die Schreibweise $T\,[\textrm{K}]$, dass hier die Temperatur in Kelvin eingesetzt werden muss. Die Wellenlänge des Strahlungsmaximums $\lambda_{\textrm{max}}$ kommt dann in $\mu\textrm{m}$ raus. Zur Erinnerung: die Kelvin-Skala entspricht der Celsius-Skala, nur, dass der Nullpunkt verschoben ist: $T\,[\textrm{K}] = T\,[^{\circ} \textrm{C}] + 273{,}15$.

Wie du bemerkst verliert das Wiensche Verschiebungsgesetz bei 0 K seinen Sinn. Null Kelvin sind der absolute Nullpunkt, bei dieser Temperatur zappeln keine Atome mehr, und es wird daher auch keine thermische Strahlung ausgesendet. Da Temperatur diesem Zappeln der Atome entspricht, ist auch keine Temperatur unter dem absoluten Nullpunkt möglich.

Aber zurück zu den Sternen: auf einem gemessenen Spektrum können wir die Wellenlänge des Strahlungsmaximums ablesen, und das Wiensche Verschiebungsgesetz gibt uns dann die Oberflächentemperatur.

Wir haben jetzt schon einiges über Sterne und Schwarzköperstrahlung erfahren. Bevor wir nun zur Beschreibung von Helligkeiten der Sterne kommen, schlagen wir dir einen kleinen Exkurs zur Mathmatik vor:

Was sind Logarithmen?

Und falls dir Logarithmen schon vertraut sein sollten:

Logarithmen kenn ich, weiter zu den Magnituden!

Wenn du lieber mehr zur Mathematik des planckschen Strahlungsgesetzes erfahren möchtest, und auch schon im ersten Modul mit Python gearbeitet hast, könntest du an dieser Stelle auch schon zu einer Bonus-Seite springen.

Letzte Aktualisierung: 2021-11-16 16:14