Modul 2 » Was sind eigentlich Logarithmen?

Logarithmen sind ein nützliches mathematisches Werkzeug, dass in allen Bereichen der Wissenschaft auftaucht. Oft werden Logarithmen verwendet, wenn gemessene Werte oder Größen einen sehr breiten Bereich überdecken. Das ist zum Beispiel sowohl bei der scheinbaren Helligkeit wie auch bei der tatsächlichen Leuchtkraft von Sternen der Fall. So senden die leuchtkräftigsten Sterne ungefähr 10'000'000'000 mal mehr Leistung ins Weltall als die schwächsten Sterne.

Zur Definition, bitte!

Wenn man Logarithmen formal definiert, klingt das abschreckend kompliziert:

"Der Logarithmus einer Zahl ist der Exponent, mit dem die Basis potenziert werden muss, um die gegebene Zahl zu erhalten".

Nähern wir uns dieser sperrigen Definition mit einem Beispiel. Nehmen wir zunächst an, es gibt ein Parameter der "Basis" heisst, und den Wert 10 hat. Was "Basis" bedeutet, werden wir gleich verstehen. Jedenfalls gilt dann:

Zahl	Logarithmus der Zahl
100	2
1000	3
10000	4
100000	5

Der Logarithmus von 100 ist 2, da man die Basis "hoch 2" nehmen muss, um 100 zu erhalten: $10^2 = 100$ . Um 1000 zu erhalten, muss man dagegen die Basis "hoch 3" nehmen, $10^3 = 1000$ , daher ist 3 der Logarithmus von 1000. Umgekehrt ist es auch einfach, von einem Logarithmus-Wert wieder die ursprüngliche Zahl zu errechnen: wenn der Logarithmus z.B. gleich 4 ist, nimmt man dafür einfach die Basis "hoch 4", und bekommt $10^4 = 10000$ .

Logarithmus als Funktion

Wie das Beispiel gezeigt hat, ist der Logarithmus einer Zahl eine andere Zahl. Der Logarithmus ist also das Ergebnis einer Funktion (der sogenannten Logarithmusfunktion). Wenn die Basis gleich 10 ist, wie wir hier angenommen haben, schreibt man diese Funktion $f(x) = \log_{10}(x)$ .

Vielleicht ist dir aus dem Mathematikunterricht schon bekannt, dass man auch mit nicht-ganzen Zahlen potenzieren kann. Das lässt auch dein Taschenrechner zu. So gilt zum Beispiel $10^{0{,}5} = 3{,}162278...$ , was wie erwartet zwischen $10^{0} = 1$ und $10^{1} = 10$ liegt.

Die Logarithmusfunktion, die das Potenzieren ja in gewisser Weise umkehrt, kann demnach auch genau so gut auf alle (positiven) nicht-ganzen Zahlen angewendet werden. Entsprechend dem eben gezeigten Beispiel ergibt $\log_{10}(3.162278)$ ungefähr $0{,}5$ .

So sieht die Logarithmusfunktion aus:

Und jetzt kommt der Clou

Schauen wir uns weitere Werte der Logarithmusfunktion in Form einer Tabelle an:

$x$	$\log_{10}(x)$
0.01	-2
0.1	-1
0.5	-0.30103...
1	0
5	0.69897...
50	1.69897...

Anhand dieser kleinen Tabelle können wir eine bemerkenswerte Eigenschaft von Logarithmen beobachten. Wenn die Zahl $x$ zehn mal größer wird, steigt der entsprechende Logarithmus-Wert "nur" um die Zahl 1 an, ganz egal welchen Wert $x$ davor hatte!

So ist 50 zehn mal größer als 5, und $\log_{10}(50)$ = $\log_{10}(5) + 1$ . Die Differenz zwischen $\log_{10}(5)$ und $\log_{10}(0{,}5)$ beträgt tatsächlich auch 1, ebenso wie die Differenz zwischen $\log_{10}(0{,}1)$ und $\log_{10}(0{,}01)$ .

Wenn die Zahl $x$ sich nun um einen Faktor 100 vergrößert (also zum Beispiel von $x = 0{,}5$ auf $x = 50$ ), entspricht das zwei 10-fach-Vergrößerungen hintereinander. Folglich steigt der Logarithmus in diesem Falle um 2.

Logarithmen verwandeln also eine Multiplikation (wie z.B. "mal 10") in eine Addition ("plus 1"). Diese geniale Eigenschaft kann mit folgender Gleichung mathematisch formuliert werden:

Die Summe zweier Logarithmen ist also der Logarithmus des Produktes. Eine ähnliche Gleichung gibt es für die Differenz zweier Logarithmen:

Die Differenz zwischen den Logarithmen $\log_{10}(a)$ und $\log_{10}(b)$ wird also nur durch das Verhältnis $a/b$ bestimmt. Genau wie wir es in der obigen Tabelle beobachtet hatten. Auch für Potenzen gibt es ein Logarithmusgesetz:

Eine Potenz $\log_{10}(a^b)$ im Logarithmus ist also nichts anderes, als das Produkt des Exponenten $b$ mit dem Logarithmus der Basis $a$ .

Wir werden diese Gleichungen mehrmals in diesem Projekt nutzen, sie sind essentiell für den Umgang mit Logarithmen.

Herleitung

Die Herleitung dieser fundamentalen Eigenschaften der Logarithmen ist nicht kompliziert, daher laden wir dich ein ihr kurz zu folgen. Zunächst müssen wir folgendes verstehen:

10^{\log_{10}(a)} = a.

Das ergibt sich daraus, dass die Logarithmusfunktion die Umkehroperation des Potenzierens ist. Falls du daran zweifelst, teste diese Gleichung z.B. mal mit $a = 100$ . Wenn du mit der Gleichung einverstanden bist, dann dürfen wir sie auch links und rechts mit zwei anderen gleichen Größen multiplizieren, und bekommen so:

10^{\log_{10}(a)} \times 10^{\log_{10}(b)} = a \times b.

Den linken Teil können wir nun umschreiben, denn du kennst sicherlich die Eigenschaft des Potenzierens $10^x \times 10^y = 10^{x+y}$ . Das ergibt dann:

10^{\log_{10}(a) + \log_{10}(b)} = a \times b.

Jetzt wenden wir links und rechts die Logarithmusfunktion an, und bekommen

\log_{10}\left(10^{\log_{10}(a) + \log_{10}(b)}\right) = \log_{10}(a \times b).

Der linke Teil kann nun wiederum vereinfacht werden, da die Logarithmusfunktion das Potenzieren umkehrt. Wir können diese Operationen also einfach streichen, und bekommen damit das erste verblüffende Ergebnis:

\log_{10}(a) + \log_{10}(b) = \log_{10}(a \times b)

Nun wollen wir auch noch die Differenz zweier Logarithmen herleiten. Dazu nehmen wir diese letzte Gleichung und ersetzen $a$ durch $a/b$ :

\log_{10}\left(\frac{a}{b}\right) + \log_{10}(b) = \log_{10}\left(\frac{a}{b} \times b\right).

Den rechten Teil können wir vereinfachen:

\log_{10}\left(\frac{a}{b}\right) + \log_{10}(b) = \log_{10}(a).

Und jetzt müssen wir nur noch $\log_{10}(b)$ abziehen, und erhalten die gewünschte Formel

\log_{10}\left(\frac{a}{b}\right) = \log_{10}(a) - \log_{10}(b).

Und das war es, was wir herleiten wollten.

Log oder Ln: unterschiedliche Basen

Es sei kurz erwähnt, dass es "mehrere" Logarithmen gibt, die sich durch den Wert der Basis unterscheiden. Wir werden hier nur den Logarithmus in der Basis 10 nutzen. Die obige Gleichung haben wir daher auch in der Basis 10 geschrieben, sie ist aber generell auch für alle anderen Basen gültig. Man könnte also die drei $\log_{10}$ z.B. jeweils durch $\log_{2}$ ersetzen.

Auf einem Taschenrechner sind Logarithmen meistens in zwei Basen direkt verfügbar, mit Tasten die oft "Log" und "Ln" heissen. Dabei ist "Log" der Logarithmus in der Basis 10, und "Ln" der sogenannte natürliche Logarithmus, in einer anderen Basis. Wenn du numpy beim Programmieren mit Python verwendest, denk daran dass der Logarithmus in der Basis 10 hier np.log10 heisst, und nicht np.log (der dem natürlichen Logarithmus entspricht)!

Und was ist eine "logarithmische Darstellung" in Diagrammen?

Logarithmen erlauben es, Größen (also Zahlen) die sich um ein vielfaches unterscheiden trotzdem gut auf einer einzigen Skala darstellen zu können.

Diese Eigenschaft ist grade in Diagrammen sehr nützlich. In der sogenannten logarithmischen Darstellung wird die Position eines Punktes im Diagramm durch den Logarithmus seines Wertes bestimmt, und nicht direkt durch diesen Wert.

Sehen wir uns ein Beispiel an. Hier ist eine logarithmische Darstellung des plankschen Strahlungsgesetzes, bei verschiedenen Temperaturen:

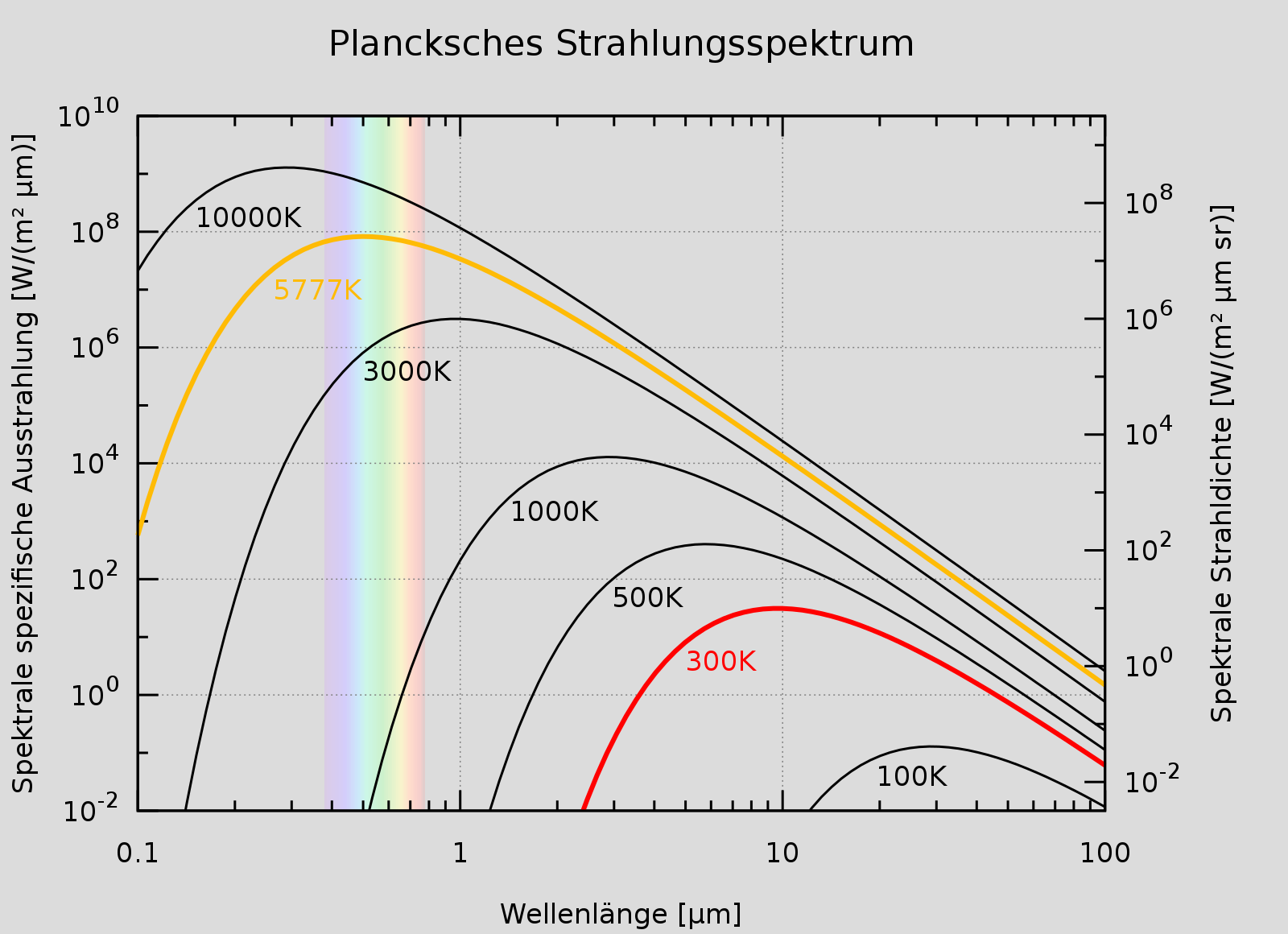
Schwarzkörperstrahlung für verschiedene Temperaturen (Sonne in gelb, Zimmertemperatur in rot), doppellogarithmisches Diagramm.

Auf der x-Achse sieht man die Wellenlänge, auf der y-Achse die abgestrahlte Leistung. Beide Achsen sind logarithmisch dargestellt. Das erkennst du daran, dass die regelmäßigen Abstände, in denen die Achsen beschriftet sind, jeweils einer Multiplikation des Wertes entsprechen. So finden wir auf der x-Achse in gleichen Abständen die Werte 1, 10, und 100, die also jedesmal um einen Faktor 10 größer werden. Das gleiche gilt für die y-Achse, daher nennt man das auch eine "doppellogarithmische" Darstellung.

Der große Nutzen dieser Darstellung wird klar, wenn du das obige Diagram mit dem der vorherigen Seite vergleichst. Bis auf die logarithmische Darstellung sind diese Diagramme tatsächlich identisch! Allerdings konnten ohne logarithmische Darstellung die Kurven für 10000 K und 3500 K praktisch nicht auf einem Diagram dargestellt werden. Dagegen passt in der doppellogarithmischen Version sogar die Kurve für 100 K bestens ins Bild.

Wie du allerdings auch bemerkst, ändert sich durch die logarithmische Darstellung auch die "Form" der Kurven, da diese nun verzerrt sind. Wegen der großen Vorteile der logarithmischen Darstellung ist das aber einfach hinzunehmen.

Weiter geht's zu den Magnituden

Letzte Aktualisierung: 2022-06-20 10:38