Gasdichteverteilung

  Ivan King bestimmte 1962 ein empirisches Dichtegesetz für Sterne in Kugelsternhaufen [KING 1962]. Dieses Gesetz überträgt man näherungsweise auf die Galaxien in Galaxienhaufen und erhält als analytische Form das sogenannte King-Profil

 

wobei 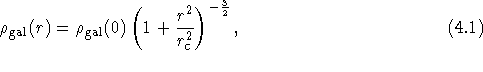die Galaxiendichte im Abstand r vom Zentrum und der Kernradius ist. Behandelt man nun das Gas als isothermes, ideales Gas und setzt hydrostatisches Gleichgewicht voraus, dann folgt Kugelsymmetrie und es gilt die hydrostatische Gleichung

 

P= Druck
G= Graviationskonstante
Gesamtmasse innerhalb von r,

und es folgt bei analoger Behandlung der Galaxien

 

mit

 

mittleres Molekulargewicht
Protonmasse
Geschwindigkeitsdispersion entlang der Sichtlinie
k= Boltzmann Konstante
Gastemperatur

[CAVALIERE & FUSCO-FEMIANO 1976, Kap. 2,], [GORENSTEIN et al. 1978, Kap. IIa,]. Gleichung 2.4 zeigt, daß das Verhältnis zwischen der spezifischen kinetischen Energie der Galaxien und des Gases beschreibt. Mit dem King-Profil (Gl. (2.1)) und Gl. (2.3) ergibt sich für das radiale Gasdichteprofil das sogenannte -Modell

 

Setzt man ein Gasgemisch von 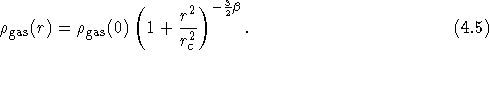Helium und Wasserstoff voraus, das aufgrund der hohen Temperatur vollständig ionisiert ist, dann gilt

 

und somit

 

wobei 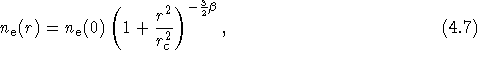die Anzahldichte der Elektronen ist.

Die Flächenhelligkeitsverteilung und somit das Aussehen eines Galaxienhaufens wird im wesentlichen durch die Gasdichteverteilung bestimmt. Um den Bezug zu der beobachtbaren Größe der Flächenhelligkeit herzustellen, werden nun einige weitere wichtige Größen eingeführt. Als Leuchtkraft wird die Gesamtleistung bezeichnet, die das System bei der Frequenz ausstrahlt. Es gilt

 

wobei

 

Emissivität
Anzahldichte der Wasserstoffionen
Emissionskoeffizient.

Für das Emissionsmaß gilt

 

Der Emissionskoeffizient hängt ab von der Gastemperatur und der Metallizität A, d. h. von der Häufigkeit von Elementen schwerer als Helium. Der Koeffizient variiert im ROSAT-Energiebereich (Abschnitt 2.3) im relevanten Temperaturbereich ( ) nur schwach (Abb. 2.1). Für die Anzahl Photonen, die in einem definierten Energiebereich pro Sekunde und pro Quadratbogenminute vom Detektor registriert werden (Röntgenflächenhelligkeit ), gilt deshalb

  
Abbildung: Aufgetragen in nicht normierten Einheiten ist der Röntgenfluß\ (Abschnitt 4.5) eines heißen thermischen Plasmas als Funktion von , wobei und A= solare Metallizität. Die 4 Kurven zeigen den am Detektor registrierten Fluß für die Werte der Wasserstoffsäulendichte . Die Emissivität und der registrierte Fluß sind nahezu konstant im Temperaturbereich . Entnommen aus [BöHRINGER 1995a, Fig. 1,].

 

wobei entlang der Sichtlinie integriert wird (im Haufenzentrum ist l=0). Mit Gl. (2.7) folgt

 

Dieses Integral läßt sich in eine Form bringen, die in [BRONSTEIN & SEMENDJAJEW 1980, Integral Nr. 39,] gelöst ist, und man erhält

 

Es ist zu beachten, daß R den an die Hemisphäre projezierten Radius darstellt. hängt ab von , , , und der Rotverschiebung z (Abschnitt 2.2). Die Annahmen, die auf diese Gleichung führen sind

• hydrostatisches Gleichgewicht
• ideales, isothermes Gas
• isotrope Geschwindigkeitsverteilung der Galaxien
• konstante Metallizität.

Bei dem späteren Bestimmen der Gas- und Gesamtmasse gehen mögliche Abweichungen von der Kugelsymmetrie und vom hydrostatischen Gleichgewicht am stärksten ein. Für eine Diskussion siehe Abschnitt 2.1.3.

Im allgemeinen läßt sich diese parametrisierte Form der Flächenhelligkeit gut an die Beobachtungsdaten anpassen (Abschnitt 4.3). Mit den dadurch bestimmten Parameterwerten von , und läßt sich sodann das Gasdichteprofil nach Gl. (2.5) bestimmen, wobei sich aus und Gl. (2.6) ergibt. Das -Modell wird seit vielen Jahren erfolgreich benutzt, es gibt aber natürlich auch andere Modelle, wie z. B. das sogenannte Navarro-Frenk-White (NFW)-Profil [NAVARRO et al. 1997, Gl. (1),], das sich bei N-Körper-Simulationen für unterschiedliche kosmologische Szenarien als gute Beschreibung erwiesen hat.

Bei einigen Galaxienhaufen findet man einen zentralen Flächenhelligkeitsexzeß (Abb. 4.10). Um diese Eigenschaft besser beschreiben und eine genauere Gasdichte bestimmen zu können, habe ich ebenfalls ein Doppel- -Modell der Form an die Beobachtungsdaten angepaßt: ein simultaner Fit von 2 -Modellen, wobei eine Komponente zur Beschreibung der gesamten Haufen-Emission und die andere zur Beschreibung des zentralen Flächenhelligkeitsexzesses dient. Es ergibt sich aus der Proportionalität (2.11), daß sich die Gasdichte dann berechnen läßt aus .