Der Versuch selbst einer kurzgehaltenen Einführung in die Grundlagen der Kosmologie würde den Rahmen dieser Arbeit sprengen. Dieser Abschnitt beschränkt sich daher auf die Einführung der für die vorliegende Arbeit benötigten Größen und Gleichungen. Standardwerke zum Thema können dem Literaturverzeichnis entnommen werden, z. B. [MISNER et al. 1995], [PADMANABHAN 1993], [PEEBLES 1993], [WEINBERG 1972].
Das derzeit am häufigsten verwendete Modell zur Beschreibung der Raumzeit ist das Friedmann-Robertson-Walker-Modell. Die Metrik dieses Modells hat das Linienelement
c= Vakuumlichtgeschwindigkeit
R(t)= Skalenfaktor zur kosmischen Zeit t
k= { 
} Krümmungsindex
mitbewegte Kugelkoordinaten
[WEINBERG 1972, Gl. (14.2.1),], von hier an (We).
Für die physikalische Entfernung d zweier Objekte auf der
Hypersphäre konstanter kosmischer Zeit erhält man demnach
Für ein flaches Universum (k=0) folgt
Daher ist das physikalische Volumen einer Kugel mit Radius d gegeben durch
Die Rotverschiebung z vergleicht die im Beobachtersystem gemessene
Wellenlänge 
eines Photons mit der im Ruhesystem des
Objekts emittierten Wellenlänge 
über
Ursache der Rotverschiebung ist die Änderung des Skalenfaktors
zwischen dem
Zeitpunkt der Emission 
und der Absorption im Detektor 
. Deshalb hat man
(We, (14.3.5 und 6)).
Die Leuchtkraftentfernung 
ist definiert als
wobei 
der vom Beobachter registrierte bolometrische
Energiefluß und 
die pro Sekunde vom Objekt emittierte
Energie darstellt. Weiterhin gilt
(We, (14.4.13 und 14)).
Die Hubble-Konstante 
, der Abbremsparameter 
und die
kritische Dichte 
sind definiert als (We,
(14.6.2 und 3), (15.2.3))
Weitere exakte Beziehungen ergeben sich durch
die Kombination der Friedmann-Robertson-Walker-Metrik mit den
Einsteinschen Feldgleichungen. Mit einem kosmischen
Druck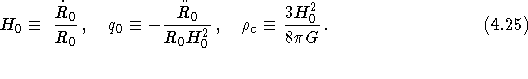 
, einer kosmologischen Konstante 
und 
sind dann
die Größen r, 
und z über die
Mattig-Gleichung verknüpft
(We, (15.3.23)). Für ein flaches Universum mit obigen
Voraussetzungen gilt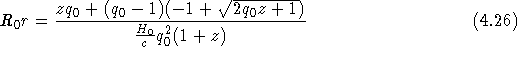 
und damit
Mit Gl. (2.24) erhält man somit
Neben den bereits erwähnten Voraussetzungen gilt in dieser Arbeit, soweit nicht anders angegeben,
