Daten

  Bei der Ermittlung der Gastemperaturen von Haufen, für die in den angegebenen Quellen keine Temperaturen angegeben sind, wurde die Relation von [MARKEVITCH 1998, von hier an (Ma),] benutzt (Abschnitt 4.4). Mit den in dieser Arbeit bestimmten Leuchtkräften und verwendeten Gastemperaturen kann ebenfalls eine Relation aufgestellt und mit der vorher benutzten verglichen werden. In Abb. 6.4 ist in Abhängigkeit von für 55 Galaxienhaufen aufgetragen. Haufen, deren Temperatur mit der Relation bestimmt wurde, sind nicht eingezeichnet. Ebenso wurden Haufen mit ausgeschlossen, da solche in der Stichprobe von (Ma) ebenfalls nicht vorkommen. Es wurde eine lineare Regression an die logarithmisch aufgetragenen Datenpunkte durchgeführt und die sich ergebende Gerade im Bereich der Datenpunkte eingezeichnet. Ebenfalls eingezeichnet ist die Relation von (Ma). Die Werte für die Steigung und den Achsenabschnitt sind bei beiden Geraden nahezu identisch.

  
Abbildung: Die Leuchtkraft in Abhängigkeit der Gastemperatur für 55 Galaxienhaufen. Ausgenommen sind alle Haufen, deren Temperatur mit der Relation bestimmt wurde, die Haufen Abell 3574 und Abell 3628 (Daten für diese Haufen werden in keinem Diagramm gezeigt, vgl. Tab. 4.3), sowie alle Haufen mit . Die durchgezogene Linie stellt die beste Regressionsgerade an die Datenpunkte dar. Die gestrichelte Linie ist die Relation von (Ma).

  
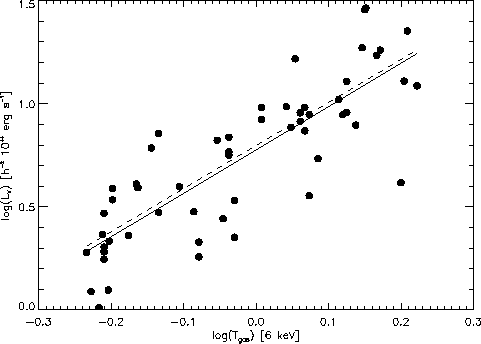
Abbildung 6.5: Die Leuchtkraft in Abhängigkeit der Gastemperatur für 74 Galaxienhaufen. Ausgenommen sind alle Haufen, deren Temperatur mit der Relation bestimmt wurde. Bedeutung der Linien wie in Abb. 6.4. Man erkennt, daß die Steigung zum leuchtschwachen Ende hin steiler wird.

Es ergeben sich für 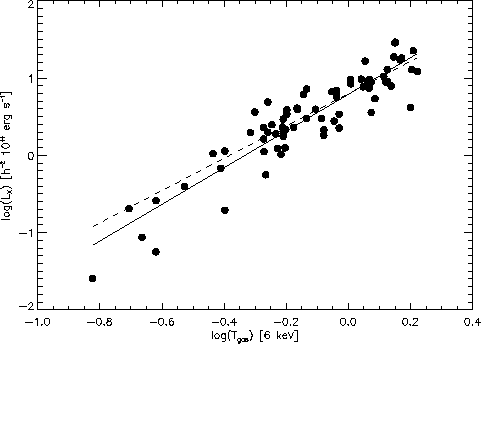, wobei und in Einheiten von und in Einheiten von gegeben sind, die Parameterwerte und . Benutzt man hingegen auch Haufen, die unter der Schranke von (Ma) von liegen (Abb. 6.5, 74 Haufen), erhält man und .

In Abb. 6.6 ist die Leuchtkraft in Abhängigkeit der Gasmasse aufgetragen. Wegen der geringen Unterschiede, der mit dem einfachen und der mit dem Doppel- -Modell bestimmten Gasmassen werden ausschließlich die ersteren verwendet. Die besten Werte für die Fitparameter für einen Fit der Form , wobei , A und die Standardabweichung in der Leuchtkraft in Einheiten von und in Einheiten der Sonnenmasse gegeben sind, lauten und . Die Standardabweichung ist .

  
Abbildung 6.9: Die Leuchtkraft in Abhängigkeit der Gasmasse für 88 Galaxienhaufen.

In Abb. 6.7 ist die zentrale Elektronenzahldichte über der Gasmasse aufgetragen. Man erkennt, daß die beiden Größen unabhängig voneinander sind. Dieser Sachverhalt könnte auf eine Relation zwischen einer relativ leicht beobachtbaren Größe und der Gesamtmasse hindeuten, da diese Unabhängigkeit und die Annahme einer Proportionalität zwischen Gasmasse und Gesamtmasse erwarten läßt, daß der Kernradius mit zunehmender Gesamtmasse steigt, da ein massiver Haufen bei gleicher zentraler Dichte weiter ausgedehnt sein muß , als ein weniger massiver. Dies wird durch den Graphen in Abb. 6.8 bestätigt. Eine lineare Regression an die logarithmisch aufgetragenen Datenpunkte liefert die Kernradius-Gesamtmasse Relation 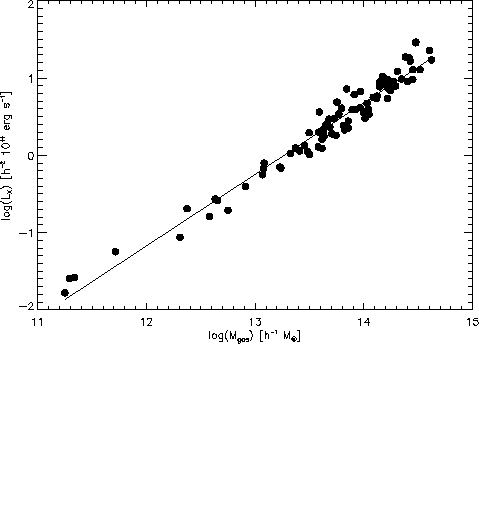. Eine Aussage über die Verläßlichkeit einer Gesamtmassenbestimmung mittels dieser Relation wird in Abschnitt 6.2.3 getroffen.

  
Abbildung: Zentrale Elektronenzahldichte in Abhängigkeit der Gasmasse für 88 Galaxienhaufen. Man erkennt, daß die zentrale Elektronenzahldichte unabhängig von der Gasmasse ist. Die Benutzung von zentralen Dichten, die mit dem Doppel- -Modell bestimmt wurden, ändert an dieser Aussage nichts. Die Streuung zwischen Elektronen pro ist durch die unterschiedlichen zentralen Flächenhelligkeiten bedingt, die als Dichteschwankungen infolge unterschiedlich starker Cooling Flows interpretiert werden können.

  
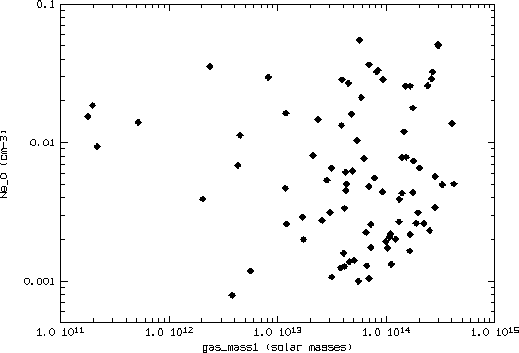
Abbildung 6.8: Der Kernradius in Abhängigkeit der Gesamtmasse für 88 Galaxienhaufen. Die Streuung spiegelt die Streuung in der zentralen Dichte wieder. Man beachte jedoch auch die in Abschnitt 5.3 abgeschätzten, nicht eingezeichneten, Fehler für die Gesamtmassenbestimmung von bis zu einem Faktor zwei.

  
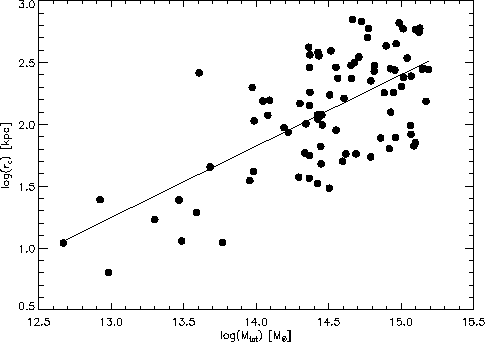
Abbildung: Die Leuchtkraft in Abhängigkeit der Gesamtmasse für 88 Galaxienhaufen.

Eine Relation mit geringerer Streuung besteht zwischen der Röntgenleuchtkraft und der Gesamtmasse (Abb. 6.9). Die besten Werte für die Fitparameter für einen Fit der Form 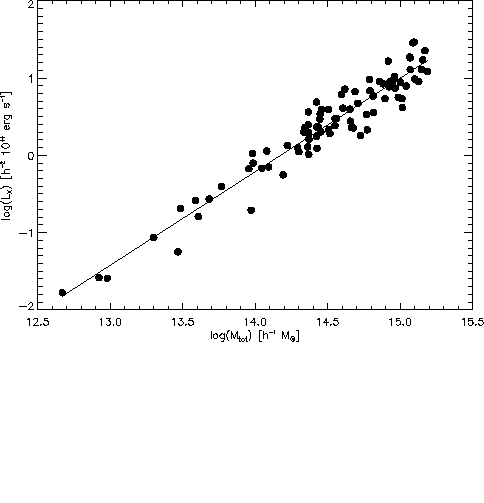, wobei , A und in Einheiten von und in Einheiten der Sonnenmasse gegeben sind, lauten und . Die Standardabweichung ist .

In Abb. 6.10 ist die Gastemperatur in Abhängigkeit der Gesamtmasse aufgetragen. Man muß dabei im Auge behalten, daß bei der Bestimmung der Gesamtmasse mit Hilfe von Gl. (5.3) die Temperatur linear eingegangen ist, und also nicht unabhängig voneinander bestimmt worden sind. Dennoch macht es Sinn, hier die Relation zu bestimmen, da bei Anwendungen dieser Relation bisher oft auf theoretische Herleitungen zurückgegriffen wird (Abschnitt 6.2.2).

  
Abbildung 6.11: Die Gastemperatur in Abhängigkeit der Gesamtmasse für 74 Galaxienhaufen. Galaxienhaufen, deren Gastemperatur mit der Relation bestimmt wurden, wurden ausgeschlossen.

Die besten Werte für die Fitparameter für einen Fit der Form 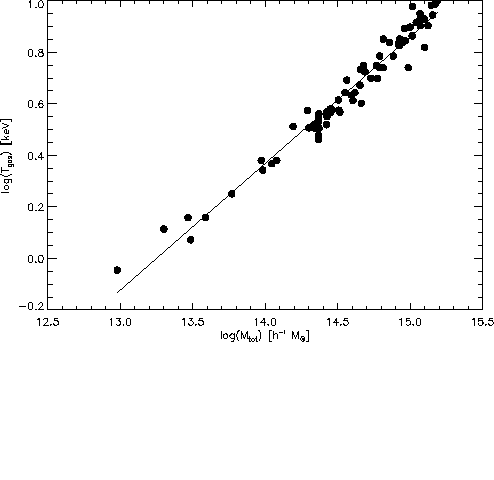, wobei und A in Einheiten von keV und in Einheiten der Sonnenmasse gegeben sind, lauten und .

Nahezu unabhängig voneinander bestimmt sind hingegen Gasmasse und Temperatur. Eine lineare Regression an die logarithmisch aufgetragenen Datenpunkte in Abb. 6.11 liefert die Temperatur-Gasmasse Relation , Einheiten wie bei der Relation.

  
Abbildung: Die Gastemperatur in Abhängigkeit der Gasmasse für 74 Galaxienhaufen. Galaxienhaufen, deren Gastemperatur mit der Relation bestimmt wurden, wurden ausgeschlossen.

Beim Bestimmen von in Abschnitt 5.1.1 wurde ein Anteil der Gasmasse an der gesamten gravitativen Masse von 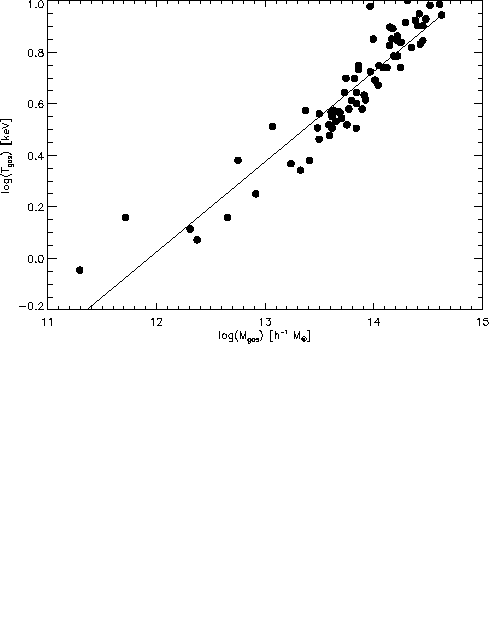angenommen. Mit Hilfe der nun bestimmten Größen ist es möglich, diese Annahme zu überprüfen. In Abb. 6.12 ist das Verhältnis von Gasmasse zu Gesamtmasse, bestimmt jeweils bei , in Abhängigkeit der Gasmasse für 88 Haufen aufgetragen.

  
Abbildung 6.12: Das Verhältnis von Gasmasse zu Gesamtmasse in Abhängigkeit der Gasmasse für 88 Galaxienhaufen.

Beim Anpassen einer Regressionsgeraden ergaben sich die Parameterwerte, so daß 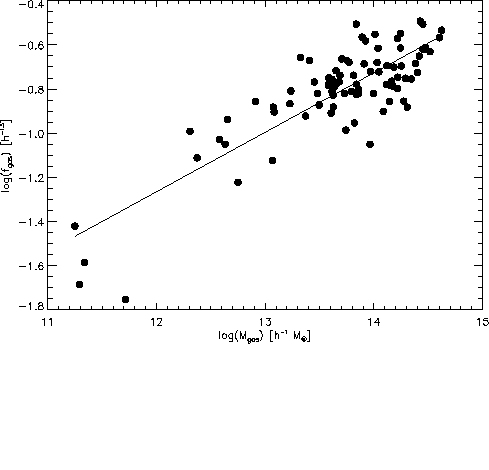, wobei in Einheiten der Sonnenmasse gegeben ist. Für die Abhängigkeit von der Gesamtmasse erhält man .

Jedoch ist es angebracht, auch an dieser Stelle noch einmal auf die Fehler in der Gesamtmassenbestimmung (nicht eingezeichnet) hinzuweisen, die in Abschnitt 5.3 abgeschätzt wurden. Sie betragen bis zu einem Faktor 2.

Um diesen relativ großen möglichen Fehler der Gesamtmassenbestimmung nicht in die Gasmassenbestimmung einwirken zu lassen, war in Abschnitt 5.1.1 der konstante Wert von für die zur Bestimmung von benötigte mittlere Gesamtdichte angenommen worden. Aus dem nun bei einigen Haufen angedeuteten geringeren Gasanteil folgt, daß bei diesen Haufen zu klein bestimmt wurde (vgl. Abschnitt 5.1.1) und damit die Gasmasse bei dem angegebenen Radius zwar relativ genau bestimmt ist, aber in bezug auf die angestrebte Vergleichbarkeit von Galaxienhaufen unterschiedlicher Größe etwas zu niedrig ist.

Bei möglichen unterschiedlichen Abhängigkeiten der Gas- und Gesamtdichte vom Radius könnte aus diesen Gründen auch die Vergleichbarkeit der bestimmten Gasanteile einiger Haufen leicht eingeschränkt sein.