



Next: Computation
Up: Imaging
Previous: Spectral Line Imaging
Each visibility sample is given a weight in the imaging step. This weighting
can be used to account for differences in the density of sampling in
different parts of the u-v
plane, or to account for different noise
variances in different samples, or to improve sensitivity to extended
objects, etc. Here we briefly review some weighting schemes:
- Natural weighting
- This gives constant weights to all
visibilities (or, more strictly,
inversely proportional to the noise variance of a visibility). This weighting
gives optimum point-source sensitivity in an image. However the synthesised
beamshape and sidelobe levels are usually poor.
- Uniform weighting
- This gives a weight inversely proportional to
the sampling density function. This form of weighting minimises the sidelobe
level. However the noise level can be a factor of 2 worse than natural
weighting.
- Super- and sub-uniform weighting
- Uniform weighting computes the
sampling density function on a grid that is the same size as the
gridded u-v
plane. This results in the synthesised beam sidelobes
being minimised over the same field-of-view as the region being
image. Surprisingly, making the field-of-view very large (bigger than
the primary beam size) or very small (comparable to the synthesized beam)
both cause uniform weighting to reduce to natural weighting.
Super- and sub-uniform weighting decouple the weighting from the field size
being imaged. Instead, the sidelobes in the synthesised image are minimised
over some arbitrary field size, with this field being either smaller or
larger than the field being imaged (for super- or sub-uniform weights
respecitvely).
- Robust weighting
- Uniform weighting (including super- and sub-uniform
weighting) minimising sidelobes, whereas natural weighting minimises
the noise level. Robust weighting provides a compromise between the two,
doing so in an optimal sense (similar to Wiener optimisation).
See Dan Briggs' thesis
for more information.
- Tapering
- In signal processing theory, the optimum way to
detect a signal of known form, which is buried in noise, is to convolve that
signal with a ``matched filter''. This filter has an impulse response which
is just the reverse of the form of the signal that is being detected.
Applying
this principle to detecting sources in radio interferometry, the optimum
weighting for detecting
a Gaussian source is to weight the visibility data
by a Gaussian. This is often called `tapering'. Using a Gaussian weight
will significantly increase the detectability
of an extended source. However it also degrades the resolution. Gaussian
weighting can be combined with any of the above weighting schemes to
achieve some form of balance between sidelobes and sensitivity.
MIRIAD
gives good (excessive?) control over the visibility
weighting schemes, via three parameters and one option.
- fwhm controls tapering of the data. Unlike AIPS
, this taper
is specified in the image domain, in arcseconds.
If you are interested in
features of a particular angular size, then the signal-to-noise ratio in the
resultant dirty image is optimized for these features if the taper FWHM is
the same as the source FWHM (or source scale size).
- sup is used to control super- and sub-uniform weighting.
The sup parameter indicates the region of the dirty beam
(centered on the beam centre) where sidelobes are to be suppressed or
minimised. Like the
fwhm parameter, the sup parameter is
given in arcseconds. The weights that invert
calculates are
optimal, or near optimal, in a least-squares sense to minimising
the sidelobes in the specified region of the beam. Although the
sidelobe suppression region is not a direct control of resolution and
signal-to-noise ratio, it does have an effect on these
characteristics.
Suppressing sidelobes over the entire field of the dirty beam
corresponds to uniform weighting -- that is, we get uniform weighting if
sup is set to the field size of the dirty beam; this is the
default. Alternately making no attempt to
suppress sidelobes ( sup=0) corresponds to natural weighting.
Increasing sup from 0 to the field size results initially in an
improvement in resolution until the value of sup is approximately
equal to the best resolution. Increasing sup beyond this results
in a slow degradation in resolution. The noise level varies in
a less regular way with sup. Apart from saying that sup=0
(natural weighting) gives the optimum signal-to-noise ratio, it is not
possible to generalise. However the noise level will be no worse than
a factor of a few from the optimum.
The default value for sup is the field size ( i.e. uniform
weighting).
- robust In MIRIAD
, robust weighting is parameterised
by a ``robustness'' parameter. Values less than about -2 correspond
essentially to minimising sidelobe levels only, whereas values greater than
about +2 just minimising noise. A value of about 0.5
gives nearly the same sensitivity as natural weighting, but with
a significantly better beam.
- options=systemp The basic weight of a visibility (the weight used
for natural weighting, or the weight used for a point in determining the
local sampling density function) is ideally
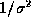 , where
, where 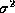 is
the noise variance of a visibility. Because historically the value for this
in a MIRIAD
data-set has been of dubuious reliability, invert
is
the noise variance of a visibility. Because historically the value for this
in a MIRIAD
data-set has been of dubuious reliability, invert
normally assumes the
noise variance is inversely proportional to the integration time of a
visibility. However ATCA data
loaded with MIRIAD
atlod
will contain good estimates of 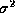 :
using the true
:
using the true 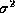 will result in some improvement in sensitivity in
the final image. In this case, the
will result in some improvement in sensitivity in
the final image. In this case, the
systemp option can instruct invert
to compute the basic
weights using 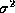 .
.




Next: Computation
Up: Imaging
Previous: Spectral Line Imaging
Last generated by rsault@atnf.csiro.au on 16 Jan 1996
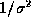 , where
, where 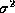 is
the noise variance of a visibility. Because historically the value for this
in a MIRIAD
data-set has been of dubuious reliability, invert
is
the noise variance of a visibility. Because historically the value for this
in a MIRIAD
data-set has been of dubuious reliability, invert
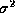 :
using the true
:
using the true 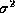 will result in some improvement in sensitivity in
the final image. In this case, the
will result in some improvement in sensitivity in
the final image. In this case, the
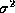 .
.