Photo-ionisation with recombinations

With recombinations (but still without dynamics) in a uniform medium we are modelling the classic Strömgren analysis. It is convenient to measure length in units of $R_s$ and time in units of the recombination time, $t_{\mathrm{rec}}=(\alpha_{rr} n_{\mathrm{H}})^{-1}$. In these units the radius of the I-front can be expressed as

$$R_{\mathrm{2D}}(t)=\sqrt{1-e^{-t}}\,,\qquad R_{\mathrm{3D}}(t)=(1-e^{-t})^{1/3}\,.$$ (2.9)

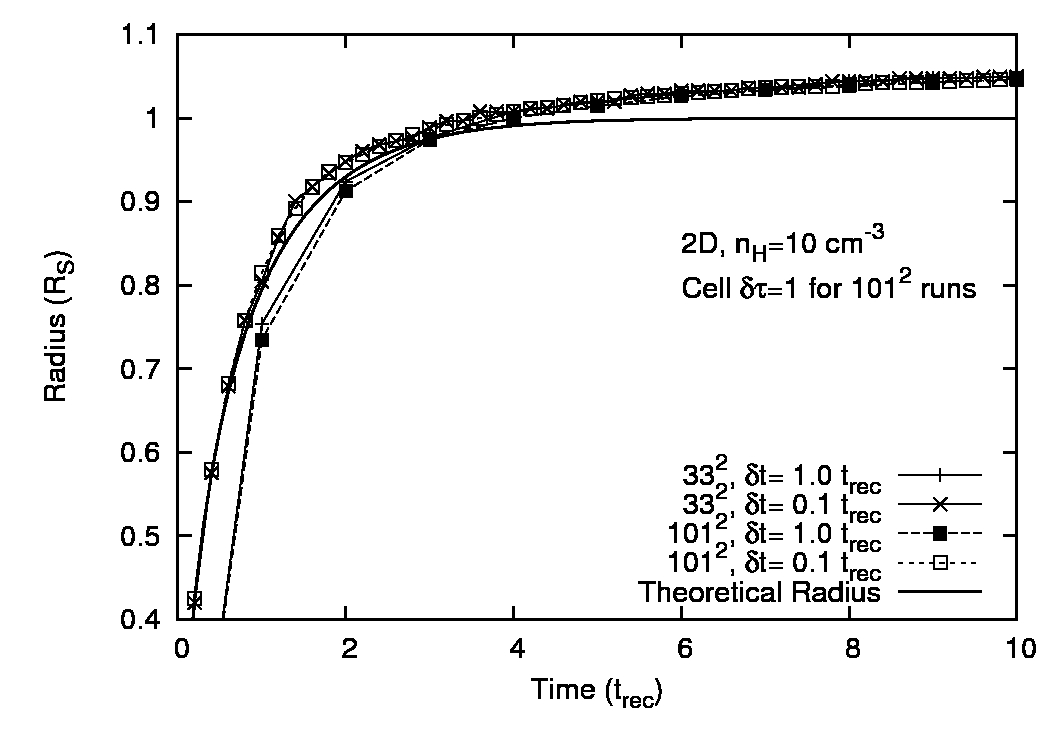
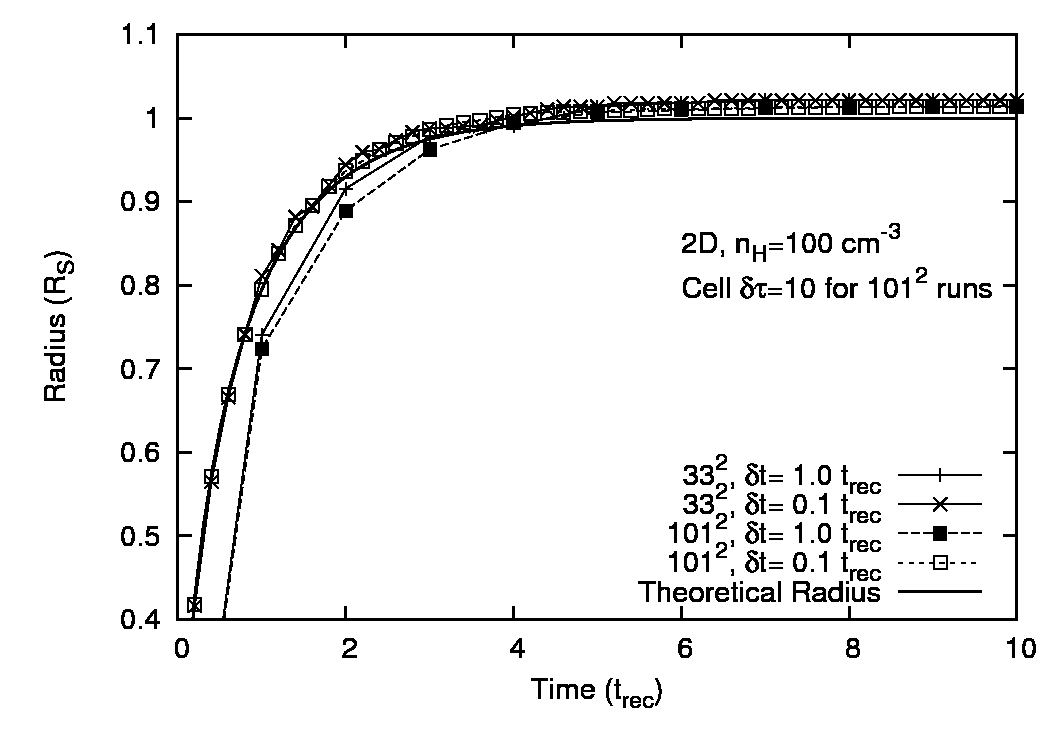
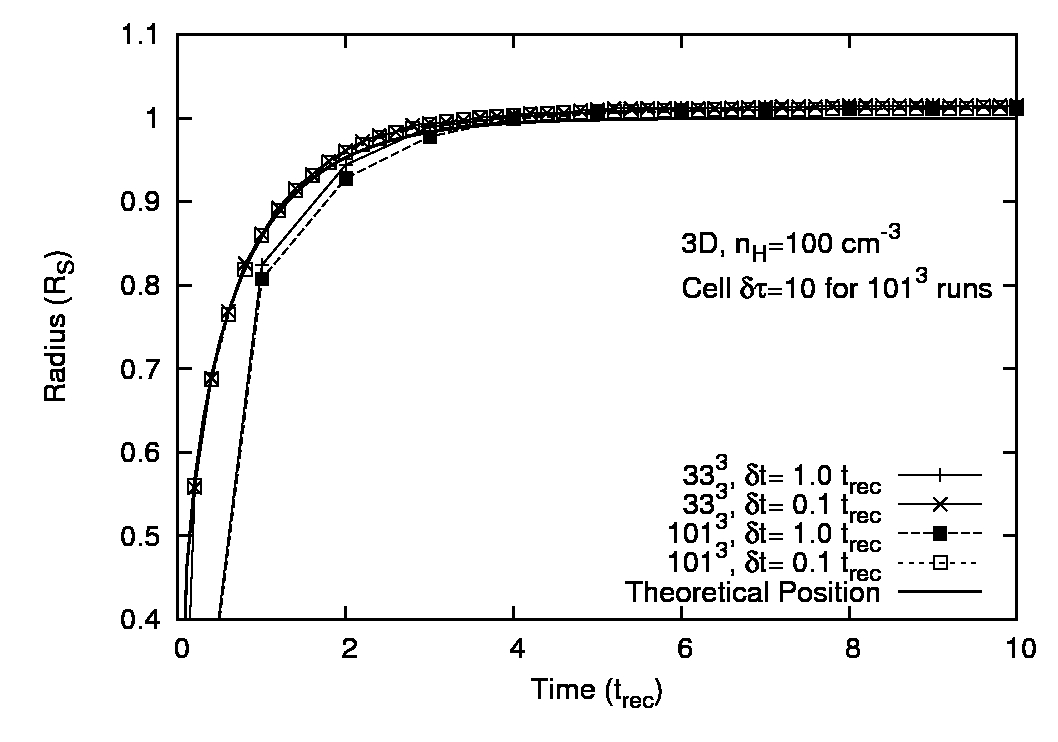
Fig. 2.14 shows the position of the I-front as a function of time for simulations with recombinations included, with the analytic solutions plotted as a solid line. Note that for the low density runs the cell optical depth is $\delta \tau =1$ and so the I-front is resolved. In this case the analytic approximation of a sharp I-front breaks down and the final radius deviates from $R_s$. For the higher density runs the I-front is unresolved and its mean position is always within $1-2$ per cent of the analytic value except at very early times when it has only crossed a few cells, or when the timesteps are of order the recombination time. This is an expected limitation of the C$^2$-ray method since it uses time-averages of the photon flux through each cell (see Mellema, 2006). For the tests where $\delta t=t_{\mathrm {rec}}$ we underestimate the I-front velocity while it expands to $R_S$. The error is slightly larger at higher spatial resolution because we have to do the same inaccurate time-average across more cells and the error is always on the side of losing photons. For sufficient time resolution, however, the I-front propagates at the correct speed, and it is worth noting that the photo-ionisation time for a cell is much shorter than the recombination time while the I-front is expanding rapidly. We do not need to resolve this timescale to get accurate results. This is the major strength of the C$^2$-ray algorithm.

Figure 2.14: These plots show the evolution of the I-front radius over time for runs with recombinations switched on. Again it is a uniform medium with the same optical depths per cell as Fig. 2.13. The time is shown in units of the recombination time $t_{\mathrm {rec}}$, and the radius in units of the Strömgren radius, $R_s$ (or its 2D analogue). When the timestep $\delta t=t_{\mathrm {rec}}$ the I-front propagates too slowly, but for $\delta t=0.1t_{\mathrm {rec}}$ it has the correct speed. The first two panels are shown for a background medium with $n_{\mathrm{H}}=10\,\ensuremath{\,\mbox{cm}^{-3}}$ corresponding to $\delta \tau =1$ per cell for the 101 cell runs. The equilibrium radius is not equal to $R_s$ because the I-front is resolved and has a thickness of a few cells. The lower two panels are shown for a background medium $10\times$ denser so the I-front is not resolved and the equilibrium radius is within a cell-width of $R_S$.