Double Mach Reflection

Test Description

This test was first described by Woodward (1984), and is also part of the Athena code (Stone, 2008) test suite^2.1. This tests the robustness of the numerical algorithms, as well as testing that shocks propagate at the correct speed in all directions (the ``carbuncle instability''). It also has reflective, inflow, and outflow boundary conditions, so if they have problems it will show up in this test. The test generates a number of shock waves and discontinuities, some of which should be straight lines, and which are at different angles to the grid axes. If the algorithm has insufficient numerical diffusion the shocks will not stay as straight lines, and in particular there will be problems near the reflection boundary.

The setup is as follows: the domain is $x=[0,3.25]$, $y=[0,1]$, with spatial resolutions of $[N_x,N_y]=[260,80]$ and $[520,160]$ grid cells. We use an ideal gas equation of state with $\gamma =1.4$ and an undisturbed gas state $[\rho,p_g,v_x,v_y]=[1.4,1.0,0,0]$. A Mach 10 shock is set up whose initial position on the lower boundary is $x=1/6$ and whose propagation direction is $30\ensuremath{^\circ}$ from the $x$-axis (moving down onto the reflecting $x$-axis). Special fixed boundary conditions are set up for $y=0$ and $x=[0,1/6]$ allowing the shock to propagate off the domain. For the upper boundary $y=1$ a time-dependent boundary is imposed to allow the shock to propagate onto the domain as though it extended to infinity.

The simulation is run until $t=0.2$, by which time the shocks should be nearly at the right edge of the domain. For these tests a Courant (CFL) number $C_{\textsc{CFL}}=0.7$ is used, with viscosity $\eta_{\mathrm{v}}=0$ or $\eta_{\mathrm{v}}=0.1$.

Figure 2.6: Contour Plots of results of the double Mach reflection test using different solvers and levels of added diffusion. These are low resolution runs with $260\times 80$ grid cells.

Figure 2.7: Contour Plots of results of the double Mach reflection test using different solvers and levels of added diffusion. These are higher resolution runs with $520\times 160$ grid cells.

Results

Contour plots have been generated from the simulation outputs at $t=0.2$ to compare with other work (Woodward, 1984; Stone, 2008). Low resolution simulations with $[N_x,N_y]=[260,80]$ are shown in Fig. 2.6 and higher resolution models with $[N_x,N_y]=[520,160]$ in Fig. 2.7. In each figure the top two panels show runs using the primitive variable based Riemann solver which uses a linearised solver for easy problems and an exact solver for difficult cases. The bottom two panels use a linearised Riemann solver with Roe-averaging of the conserved variables for the mean intermediate state (see code description). The first and third panels show runs with no artificial viscosity added, and the second and fourth show runs with the viscosity of Falle (1998) using $\eta_{\mathrm{v}}=0.1$.

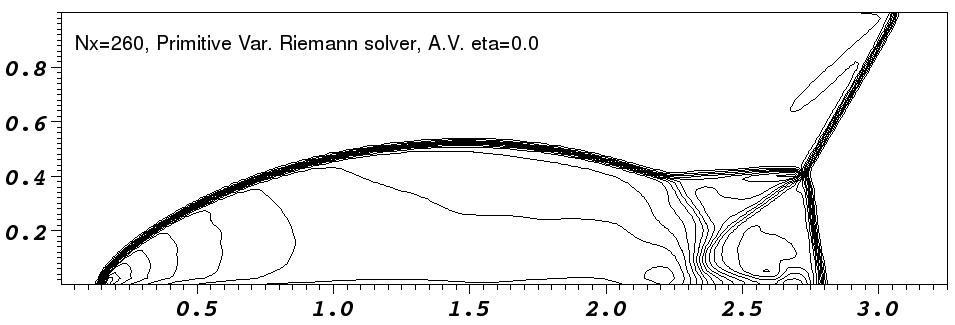
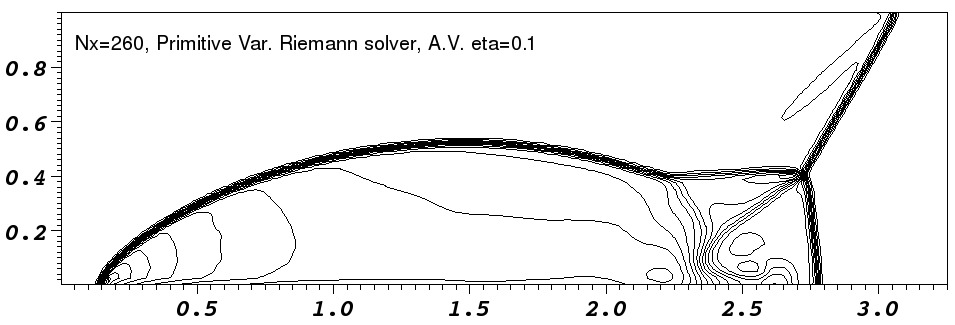
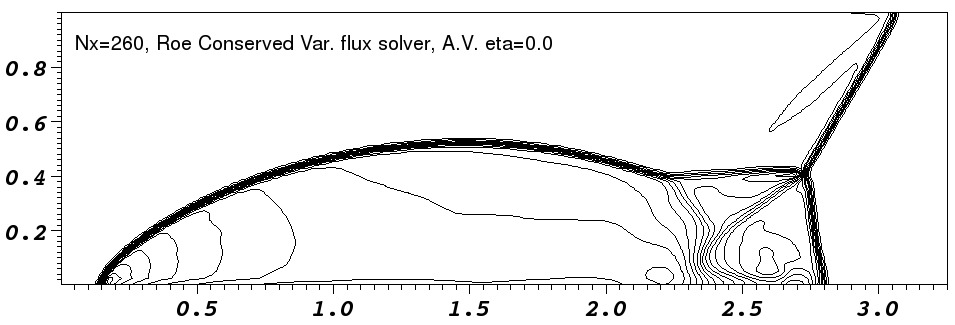
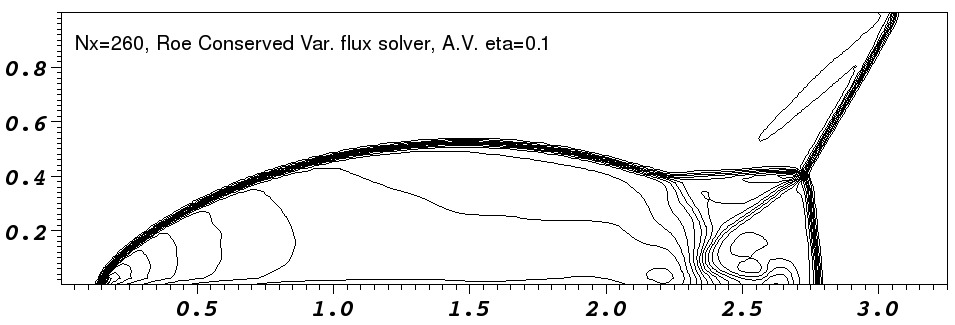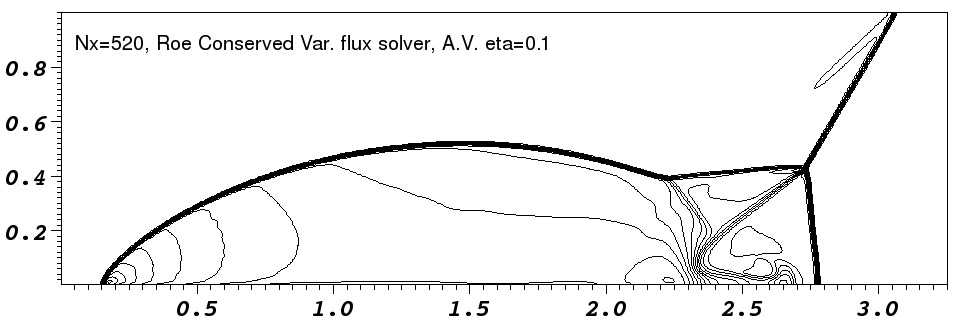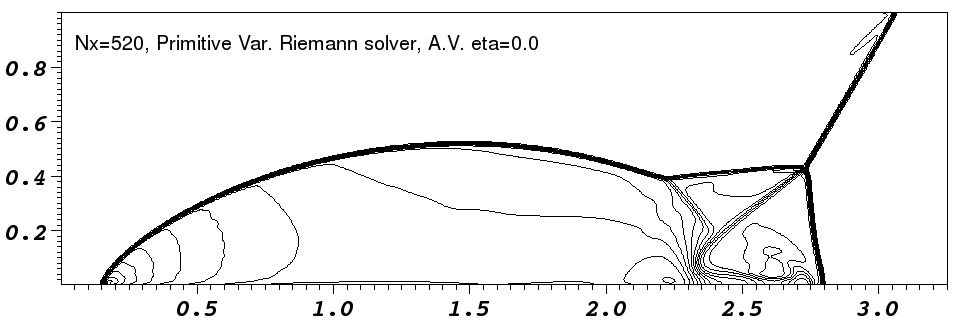
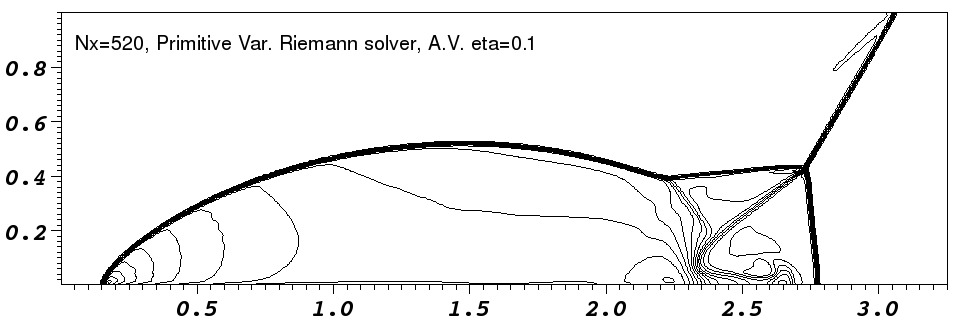
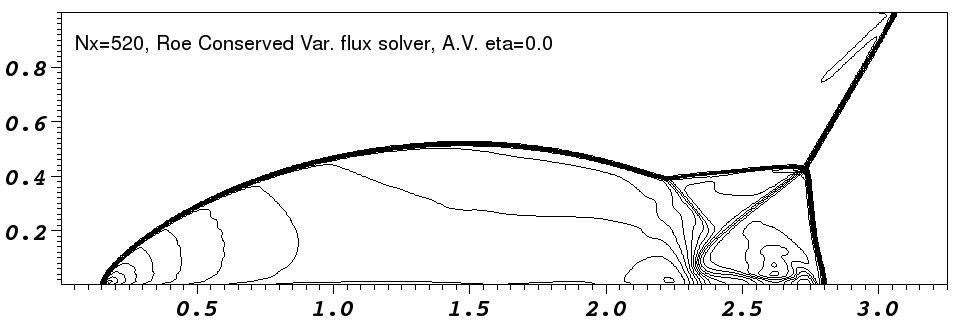
In the low resolution runs, the `jet' near the reflection axis clearly propagates further in the $x$-direction in the runs without added diffusion. This is the well known ``carbuncle'' problem and it is seen most clearly in the Roe-solver run where the shock is kinked as it approaches the $y=0$ axis. The runs with diffusion added do not have this problem at all, and the flow in other regions is largely unaffected. In particular the shocks are not much more spread out in models with extra diffusion. For the high resolution runs the shocks and other discontinuities are better resolved, as expected, and the effects of added diffusion are very similar to lower resolution runs. Comparison with fig. 16 of Stone (2008) shows that our code appears slightly more diffusive than Athena. This is particularly noticeable in the contact discontinuities.

The artefact noticeable behind the shock near $y=1$ is caused by a combination of the initial and boundary condition. The initial shock is perfectly sharp and a low amplitude startup wave is left behind it (e.g. Falle, 1998). Additionally the boundary condition has a perfectly sharp shock whereas the time integration smears the shock over a number of zones. This imperfect coupling of the artificial boundary shock to the evolving shock on the domain causes a wave to propagate into the region behind the shock. Having a more detailed boundary condition would largely remove this feature.