The Laplacian Pyramid has been developed by Burt and Adelson in 1981 [4] in order to compress images. After the filtering, only one sample out of two is kept. The number of pixels decreases by a factor two at each scale.
The convolution is done with the filter h by keeping one sample out
of two (see figure 
):
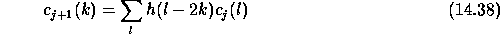
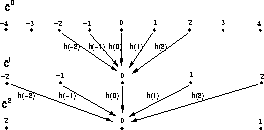
Figure: Passage from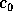 
to 
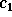, and from 
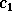to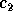 
.
To reconstruct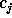 
from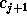 
, we need to calculate the difference
signal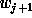 
.
where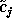 
is the signal reconstructed by the following operation
(see figure ):
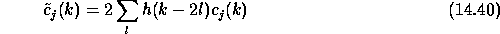
In two dimensions, the method is similar. The convolution is done by keeping one sample out of two in the two directions. We have:
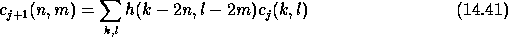
and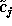 
is:
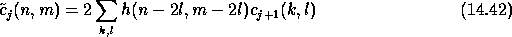
The number of samples is divided by four. If the image size is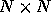 
,
then the pyramid size is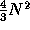 
. We get a pyramidal structure
(see figure ).
The laplacian pyramid leads to an analysis with four wavelets [3] and there is no invariance to translation.
to 
.