Der Verlauf der kumulativen Verteilungsfunktion der gemessenen
Röntgenflüsse in Abb. 6.1 stimmt sehr gut mit der
erwarteten Verteilung in einem euklidischen Universum überein. Dies
ist ein Hinweis, daß eine hohe Vollständigkeit erreicht wurde, da
bei den relativ kleinen Distanzen der Haufen in der Stichprobe starke
Effekte nichteuklidischer Geometrie nicht zu erwarten sind. Die
leichte Abweichung bei Flüssen über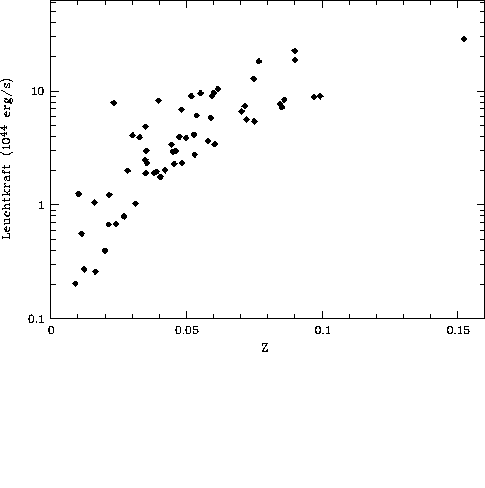 
ist wegen der kleinen Anzahl vorhandener
Haufen (4) nicht signifikant.
Die etwas geringere Steigung der Kurve relativ zur
erwarteten euklidischen Verteilung zu niedrigeren
Flüssen hin könnte auf eine mögliche geringe Unvollständigkeit
hindeuten. Ebenso kann dieser Effekt jedoch durch ungleichmäßig
verteilte Haufen, wie es bei diesen Entfernungsskalen durch groß
räumige Strukturen bedingt möglich ist,
hervorgerufen werden. Ein Indiz für diese Interpretation ist der
wieder mit einer euklidischen Neigung konforme Abschnitt zwischen 2
und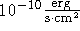 
.
Der Anstieg der differentiellen Verteilung der Rotverschiebungen in Abb. 6.2 von z=0 bis zum Maximum bei z=0.03-0.04 ist ein Volumeneffekt. Je größer das Volumen, desto mehr Galaxienhaufen findet man. Am anschließenden Abfall erkennt man, daß mit zunehmender Entfernung die Anzahl der Haufen, die über dem Flußlimit liegen, zurückgeht. Dies liegt daran, daß die Haufen nicht beliebig leuchtkräftig werden.
Den Volumeneffekt und die Flußbegrenzung erkennt man auch besonders gut in
Abb. 6.3. Der Volumeneffekt macht sich durch die mit der
Rotverschiebung ansteigende Zahl seltener, leuchtkräftiger Haufen und die
Flußbegrenzung durch die ansteigende Untergrenze der Leuchtkraft bemerkbar.
Die geringe Anzahl von Haufen mit 0.10<z<0.15 verwundert auf
den ersten Blick etwas, liegt jedoch vermutlich darin begründet,
daß die Dichte von Haufen, die ausreichend leuchtkräftig sind, bei dieser
Entfernung schon sehr gering ist.