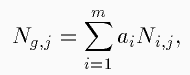1. Introduction

We are analyzing very deep F555W (V) and F814W (I) HST data using model color-magnitude diagrams (CMDs) to obtain the SFH of Leo I. Because the data are deep enough to reach the magnitude expected for the oldest turnoffs, we are able to exploit our analysis method to the maximum of its capabilities. As a result, we are obtaining a SFH with unprecedented detail, even for the earliest epoch of Leo I's evolution.

2. The data

In Fig. 1 we present the [(V-I)₀, M_I] CMD for Leo I based on the three wide field chips. It contains a total of 28 000 stars with small photometric errors (σ ≤ 0.2, chi < 1.6 and -0.5 ≤ sharp ≤ 0.5). For a more complete description of the data reduction and a discussion of the features present in the CMD, see Gallart et al. (1998a; G98a hereinafter).

3. Computing the star formation history

The model CMDs are calculated using a recent version of our synthetic CMD code, and performing a simulation of observational effects in a way similar to that described in Gallart et al. (1996a,b) and Aparicio et al. (1997a,b). To compare the model CMDs with the observed CMD, we have followed an approach similar to that of Aparicio et al. (1997b), who analyzed the dwarf galaxy LGS 3. Here, only one model CMD, with a constant star formation rate as a function of time has been computed for each pair of Z(t) and IMF. Then, this CMD has been divided into a number of age intervals to obtain what we will call partial models, ψ_i, which are simply a set of step functions with the same star formation rate per unit of time extended to a given period of time. These models are combined to produce what we call global models, which are used to search for the ψ(t) best representing the data by comparing them with the observed CMD via star counts in several regions of the CMD (see Fig. 2).

Global models have arbitrary ψ(t) functions produced by combining fractions of stars of each partial model. They do not need to be explicitly computed. Once the number of stars with which each partial model populates each of the regions defined in the CMD is known, the number of stars that populate that region for a given global model can be directly obtained as a linear combination of the form:

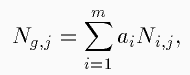
where N_g,j is the number of stars in region j for the global model, N_i,j is the same number corresponding to partial model i, a_i are the coefficients defining the global model and m is the number of partial models used. The N_g,j values are all that is needed to compare the global models with observations. An arbitrarily large number of global models can be calculated by just changing a_i: for a given set of k values of a_i, the number of global models calculated is k^m. The total star formation rate corresponding to each global model is then:

where ψ_i is the value of the star formation rate corresponding to the partial model i and l results from normalization to the observed data.

The comparison between model and observed CMDs is done through star counts in a number of CMD regions (see Fig. 2) chosen to sample stars of different ages or in specific stellar evolutionary phases. We calculate the χ² statistic of the star distribution in the r regions of the observed CMD and each global model as the indicator of the goodness of fit.

4. The particular case of Leo I. Comparison of the models with the data

We divided the model CMD into 9 partial models delineated by the age steps 15.0, 10.0, 8.0, 6.3, 4.0, 2.0, 1.0, 0.5, 0.2 and 0.01 Gyr ago and employed a set of 10 a_i coefficients. We obtained the SFH shown in Fig. 3 (dashed thin line) as the average of approximately 3000 models with the lowest values for χ². In a second step, we refined our solution by again using 10 values for each of the a_i coefficients, but choosing them this time around each average a_i coefficient obtained in the first step. This improved the resolution with which the values of ψ(t) could be estimated for each time interval. The result is shown in Fig. 3 (solid thick line), where about 3000 models (with lower values of χ²) have again been averaged. In both cases, the error bars represent the σ of the a_i values averaged to obtain ψ(t) for the time interval corresponding to the partial model.

Assuming the SFH in Fig. 3, the number of stars in each box are reproduced within a maximum error of 20% except for the box containing the HB and the one right below it (Fig. 2), for which the error is larger. The number of sub-giant stars around 1 Gyr in age is only one-fifth the number needed to reproduce the 48 stars observed in the HB area. This is due to the fact that ≅15 Gyr old stars with Z = 0.0004 do not produce a blue HB in the Padova models, and indicates that a lower metallicity is required for the old stars. When a lower metallicity is assumed for them, a ψ(t) within a factor of two of the one in Fig. 3 at the oldest epoch produces enough stars (G98b) in the HB area.

Fig. 4 shows the model CMD computed with the SFH represented in Fig. 3. It can be compared with the observed CMD in Fig. 1. The overall agreement is remarkably good, and some of the differences may be due to known weaknesses in the models discussed in G98a. These effects have been taken into account when comparing the models with the data.

5. Conclusion. The SFH of Leo I

• A major increase in ψ(t) took place around 6 Gyr ago (nearly an order of magnitude higher than the immediately preceding epoch and about a factor of 5 higher than the average ψ(t) from 15-6 Gyr ago), and lasted until about 2 Gyr ago, when ψ(t) decreased again.
• Another epoch of increased ψ(t) seems to have occurred from about 11 to 8 Gyr ago, with very little or no star formation immediately before and after.
• Star formation appears to have continued at a low rate until about 200-500 million years ago. This is necessary to account for the brightest stars in the main sequence area, and the bright yellow stars at [(V-I)₀, M_I] = (0.25, -2.0).

We are analyzing a larger number of scenarios that incorporate different assumptions for the IMF and Z(t). We expect to be able to constrain these using the same kind of analysis described here and introducing additional considerations from the best values of χ² in the different scenarios. Our preliminary results indicate that the general trend of the SFH is maintained even if the IMF and/or the chemical enrichment law are changed within reasonable limits. For a more detailed discussion of the method and an in-depth analysis of the Leo I SFH, see G98b.

References

• Aparicio A., Gallart C., Bertelli G., 1997a, AJ 114, 669
• Aparicio A., Gallart C., Bertelli G., 1997b, AJ 114, 680
• Bertelli G., Bressan A., Chiosi C., Fagotto F., Nasi E., 1994, A&AS 106, 275
• Gallart C., Aparicio A., Bertelli G., Chiosi C., 1996a, AJ 112, 1950
• Gallart C., Aparicio A., Bertelli G., Chiosi C., 1996b, AJ 112, 2596
• Gallart C., et al., 1998a, submitted to ApJ (G98a)
• Gallart C., Aparicio A., Freedman W.L., Bertelli G., Chiosi C., 1998b, in prep. (G98b)
• Knapp G.R., Kerr F.J., Bowers P.F., 1978, AJ 83, 228
• Kroupa P., Tout C.A., Gilmore G., 1993, MNRAS 262, 545
• Lee M.G., Freedman W.L., Mateo M., Thompson I., Roth M., Ruiz M.-T., 1993, AJ 106, 1420
• Stetson P.B., 1994, PASP 106, 250

• Content of the GK Workshop Proceedings
• Programme of the GK Workshop
• List of Participants
• Graduiertenkolleg - home page
• Astronomische Institute der Universität Bonn (AIUB)