Um die Argumente für die Existenz der DM verständlich zu machen, müssen zunächst die Messmethoden der Astronomie erklärt werden. Anschliessend wird über die Art der DM spekuliert, und dann auch über die Frage wo dunkle Materie versteckt sein könnte. Alle Einzelheiten der zum Teil kontrovers diskutierten Fragen zu der DM können aber in diesem Text nicht dargestellt werden.

Inhalt des Textes (mit Stichwörtern):

1. Struktur und Bewegung       a) in der Milchstrasse (Sternzählungen, Rotation der Scheibe)       b) in anderen Galaxien (Rotation ihrer Scheiben) 2. Weitere Argumente für Dunkle Materie (Galaxienhaufen: Virialmasse, Röntgenstrahlung, Gravitationslinsen) 3. Kosmologie und Dunkle Materie (Modelle für Expansion, kritische Dichte, Dichteschwankungen) 4. Hypothesen zur Natur der Dunklen Materie   (Normale Objekte;   nicht-normale Materie;   Modified Newtonian Dynamics, MOND) zu normalen Objekte: Wie könnte DM am besten versteckt sein? M Zwerge - Weisse Zwerge - Neutronensterne - Schwarze Löcher - Braune Zwerge - Planeten, Kometen, usw. Zusammenfassung 5. DM oder keine DM? (Ist die DM reell oder liegt ein Fehler in den Theorien vor? Omega-Lambda)

Betrachten wir unsere Milchstrasse, dann sehen wir eine Scheibe voller Sterne. Abseits der Scheibe gibt es weniger Sterne, und wir schauen in die weite Ferne des Universums. Bei näherer Betrachtung sind in Richtung Scheibe dunkle Stellen erkennbar. Dies ist nicht die dunkle Materie, sondern eine Verdunklung des Hintergrundsternlichtes durch staubhaltige interstellare Gaswolken.

Die Ebene der Milchstrasse zeigt viele Sterne, aber auch dunkle Stellen. Sie werden verursacht von interstellaren Gaswolken, die normalerweise etwas staubiges Material enthalten, das wie ein Nebel den Hintergrund verschleiert oder unsichtbar macht. Dieses Material ist im infraroten Teil des Spektrums hell leuchtend zu sehen. Die dunklen Stellen sind daher kein Anzeichen für Dunkle Materie. (Bild erarbeitet am STScI; Link zu Aufnahmen der Milchstrasse bei anderen Wellenlängen)

Um die Struktur unner Galaxis zu verstehen, müssen wir von den Objekten in der Galaxis die Entfernungen und die Bewegungen kennen. Nur so lässt sich ein schlüssiges Modell zur Struktur einer Galaxis entwickeln. (Einen ausführlichen Text mit Diagrammen finden Sie im Aufsatz Entschlüsselung der grossräumigen Struktur unserer Galaxis.)

Sternzählungen und Dunkle Materie

Anfang des 20.Jh wurden erneut genaue Zählungen von Sternen gemacht, um aus der räumlichen Verteilung die Struktur der Galaxis abzuleiten (insbesondere von Kapteyn in Groningen, NL). Insbesondere senkrecht zur Scheibe der Milchstrasse ist das relativ einfach, da es in dieser Richtung im Allgemeinen wenig absorbierenden Staub gibt. Man sortiert die Sterne nach Helligkeit, und benutzt dann die Abschwächung des Sternlichtes nach der normalen Entfernungsregel (1/r² mit r=Entfernung), um die räumliche Dichte in Entfernungsbereichen zu berechnen. In Wirklichkeit aber geht das nicht so einfach, da Sterne unterschiedliche Lichtmengen abstrahlen. Man muss daher eine sogenannte Leuchtkraft-Funktion hineinrechnen. Die Leuchtkraft-Funktion gibt die Verteilung der Sterne in Helligkeitsintervallen an.

Trotz dieser und anderer Komplikationen führten solche Sternzählungen zu der Vermutung, dass die beobachtete Verteilung der Sterne senkrecht zur Scheibe eine grössere durch Gravitation hervorgerufene Kraft erfordert, als man aus der Menge der bekannten Materie erklären konnte. Schon 1932 berichtet Oort über eine `Dunkle Scheibe', ein Befund, der auch nach mehr als 50 Jahren und vielen ähnlichen Studien noch von vielen Astronomen für richtig gehalten wird.

Rotation unserer Galaxis und Dunkle Materie

Galaxien rotieren um ihr Zentrum. Die Geschwindigkeit der Rotation sollte nach Kepler (wie in unserem Planetensystem) bis in grosser Entfernung vom Zentrum etwa wie r^-0.5 abnehmen. Die Rotation der Milchstrasse war schon lange aus den Bewegungen der Sterne in der Sonnenumgebung bekannt. Die Umlaufgeschwindigkeit in grossen Teilen der inneren Galaxis kann aber nicht aus Sternen gewonnen werden, da die Sterne dort eben durch staubige Gaswolken verdeckt sind.

Das in der Galaxis allgegenwärtige Wasserstoffgas strahlt im Radiobereich bei 21 cm Wellenlänge. Solche Strahlung dringt einfach durch Gaswolken hindurch. Da die Wellenlänge der Strahlung sehr gut bekannt ist, kann aus der Abweichung der Wellenlänge über den Doppler-Effekt die Geschwindigkeit der Gaswolke abgeleitet werden. Entfernungen sind so aber nicht bestimmbar. Nehmen wir nun an, dass das Gas auf Kreisbahnen um das Zentrum der Galaxis läuft. Dann hat das Gas längs eines beliebigen Sehstrahls in Richtung innere Galaxie im sogenannten Tangentialpunkt (Radiusvektor steht senkrecht zur Sehstrahlrichtung) seine grösste Dopplergeschwindigkeit. Betrachtet man nun mehrere Sehstrahlen in Scheibenrichtung, so bilden die gesammelten Bahngeschwindigkeiten und Abstände vom Zentrum an den Tangentialpunkten die sogenannte Rotationskurve.

Ein weiterer wichtiger Parameter muss noch gefunden werden: die Entfernung von der Sonne zum Zentrum der Milchstrasse. Da Sterne im Zentrum eben unsichtbar sind, benutzt man die räumliche Verteilung der Sterne im weiteren Umfeld des galaktischen Zentrums. Sterne müssen wegen der Wirkung der Schwerkraft generell etwa sphärisch (oder ellipsoidal) um das Zentrum verteilt sein. Zwei Arten von Objekten eignen sich für die Bestimmung der räumlichen Verteilung am besten, da man von beiden Typen die Entfernung relativ einfach bestimmen kann. Für die Kugelsternhaufen, die weiträumig etwa sphärisch um das Zentrum verteilt sind, findet man die Entfernung einfach aus der Photometrie: das beobachtete Farben-Helligkeits-Diagramm wird mit dem Referenzdiagramm verglichen: Der Unterschied in der Helligkeit ist entfernungsbedingt. Für den RR Lyra Typ der variablen Sterne ist die absolute (die intrinsische) Helligkeit (Mittelwert über den Lichtwechsel) konstant, so dass aus der gemessenen Helligkeit unmittelbar die Entfernung folgt. Misst man nun viele RR Lyra Sterne in einer definierten Richtung, so folgt aus den individuellen Entfernungen, wo auf dieser Strecke die Raumdichte am grössten ist. Dies muss der Punkt mit der geringsten Entfernung vom Zentrum der Milchstrasse sein.

Nach all solchen Untersuchungen weiss man, dass die Entfernung der Sonne zum Zentrum der Milchstrasse etwa 8.5 kpc (etwa 25 Tausend Lichtjahre) beträgt, und dass die Umlaufgeschwindigkeit der Sonne um das Zentrum der Milchstrasse etwa 220 km/s ist.

Nun zur DM! Normalerweise sollte die Rotationsgeschwindigkeit nach aussen in der Galaxis etwa wie r^-0.5 abnehmen. Die Beobachtungen zeigen aber eine nach aussen hin konstante Geschwindigkeit, die Rotationskurve ist `flach'. Eine flach bleibende Rotationskurve kann man verstehen, wenn die Galaxis mehr Masse enthält, als im Rotationsmodell berücksichtigt wurde. Aber für zusätzliche Masse gibt es sonst keinen Hinweis! Das heisst, auch hier braucht man DM. Und die Menge könnte gigantisch sein. Unsere Galaxis hat 1 - 2 10¹¹ Sonnenmassen (100 bis 200 Milliarden) an sichtbarer Materie, die Erkenntnisse zur DM führen, je nach Modell, zu einer 5- bis 10-fachen Menge an Materie!

b) Struktur und Bewegung in anderen Galaxien

Bei anderen Galaxien hat man den Vorteil, sie meistens komplett sehen zu können, aber den Nachteil, die Entfernungen nicht gut abschätzen zu können. Mit Hilfe der Radiosynthese-Teleskope (Gruppen gleicher Antennen, die zeitlich koordinierte Messungen durchführen) können von anderen Galaxien aber Rotationskurven gut gemessen werden. Diese Messungen reichen bis zum äussersten Rand der Scheibe des Wasserstoffgases. Solche Messungen zeigten Ende der 70-er Jahre auch bei anderen gashaltigen Spiralgalaxien flache Rotationskurven. Dort gibt es eindeutig Anlass, mehr Materie in die Modelle einzubeziehen als es `sichtbare' Materie gibt.

Eingeräumt werden muss, dass die Modellierung der Rotationskurven einiges an Freiraum lässt. So kennt man die sogenannten `maximum disk' Modelle, bei denen versucht wird, so weit wie möglich die Fehlerbereiche auszureizen, um alles mit bekanntem Scheibenmaterial zu erklären. Aber auch dann ergibt sich die Notwendigkeit der DM.

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

2. Weitere Argumente für Dunkle Materie

Die Gesamtmasse der Galaxien eines Galaxienhaufens kann aus den Bewegungen dieser Galaxien abgeleitet werden. Dabei wird der Virialsatz angewendet. Der Virialsatz besagt, dass die Summe der kinetischen Energie der Objekte einer gravitativ gebundenen Gruppe gleich der Hälfte der potentiellen Energie des Systems sein muss. Die potentielle Energie wird durch die Gesamtmasse des Systems gegeben, die summierte kinetische Energie ist aus den Geschwindigkeiten der Objekte im System zu berechnen:
        Summe (1/2 × M v²) = E(kin) = - 1/2 E(pot) = -G (Summe M)² / R     .
Die Anwendung des Virialsatzes auf Daten einiger Galaxienhaufen ergab einen Faktor 10 mal mehr Masse als man an Hand der sichtbaren Objekte erklären konnte. Also: DM!

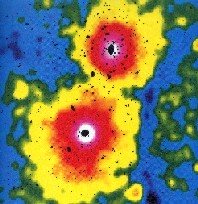
Mit Röntgensatelliten wurde ausgedehnte Röntgenstrahlung aus Himmelsgebieten um Galaxienhaufen festgestellt (Bild). Gas, das Röntgenstrahlen emittiert, muss sehr heiss sein, im Bereich von zehn Millionen Grad. Da solches Gas dünn und sehr beweglich, andererseits in Galaxienhaufen gebunden ist, muss der Haufen eine sehr grosse Schwerkraft auf dieses Gas ausüben. Dies erlaubt eine Abschätzung der Gesamtmasse des Galaxienhaufens. An den sichtbaren Galaxien des Haufens sieht man aber soviel Masse nicht. Und aus diesen Analysen folgte auch: DM!

Der Galaxienhaufen Abell 3528 zeigt bei Messungen im Röntgenbereich ein riesiges leuchtendes Gebiet. Die Farben deuten Helligkeit an, die Galaxien selber sind in schwarz über die Röntgenisophoten gemalt. Das leuchtende Gas hat eine Temperatur von etwa 10 Million Grad. Dies kann nur im Galaxienhaufen gebunden bleiben, wenn dessen Masse sehr gross ist. In diesem Fall braucht man deutlich mehr Masse, als die bekannten Massekomponenten (die in schwarz eingezeichneten Galaxien) erklären können. Ein klarer Fall für Dunkle Materie (Aufnahme ROSAT).

Grosse und massereiche Galaxienhaufen erzeugen (laut der allgemeinen Relativitätstheorie) eine lokale Raumkrümmung. Sie bewirkt, dass Licht eines Hintergrundobjektes durch die Wirkung der Gravitation abgelenkt wird. Seit den 80-er Jahren kennt man `merkwürdige' leuchtende Bögen in der Nähe von sehr massereichen Galaxien. Sie wurden 1987 als durch Gravitationslinsen erzeugte verzerrte Abbilder von Hintergrundgalaxien erkannt.

Theoretische Überlegungen erlauben, aus der Lage und Form der Bögen die Verteilung der Masse und die Gesamtmasse des Galaxienhaufens abzuleiten. Auch hier stellte sich heraus, dass weitaus mehr Masse (ein Faktor grösser als 10) anwesend ist, als Astronomen an Hand des Lichtes erklären können. Fazit: DM!

Die vom Galaxienhaufen Abell 2218 erzeugte Gravitationskraft bewirkt Verzerrung von Bildern der Hintergrundobjekte zu Punktquellen und Bögen. Aus der Form der Verzerrung und weiteren Informationen ist die Gesamtmasse des Galaxienhaufens modellierbar. Auch aus diesem Phänomen leitet man die Existenz von deutlich mehr Masse ab, als die bekannten Massekomponenten erklären können. Ein weiterer Fall für Dunkle Materie (Aufnahme HST). Link zu weiteren Gravitationslinsen vom HST

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

3. Kosmologie und Dunkle Materie

Man kann die Struktur des Universums und seine seit Hubbles Messungen dokumentierte Expansion näherungsweise in relativ einfache Gleichungen fassen. Dabei geht man von Globalparametern für das Universum aus, wie `Masse', `Radius', `mittlere Dichte', und einem Term für die Expansionsgeschwindigkeit, die der Gravitation entgegenwirkt.

Der Radius ist eigentlich der Skalenfaktor oder `Krümmungsradius' des drei-dimensionalen Raumes. Es ist nicht ein Radius im euklidischen Sinne, sondern bezieht sich auf der Länge des `geraden' Weges, den Licht in einem von der Gravitation gekrümmten Raumes zurücklegen kann.
[Es ist so etwa wie bei einer Ameise auf der Erdoberfläche. Für sie ist die Erdoberfläche eine 2-dimensionale Ebene. Die Ameise ist sehr klein und hat kein Verständnis für Erhebungen auf der Erde oder für die Krümmung der Oberfläche der Erde. Geht sie geradeaus, und einfach immer weiter, so würde sie irgendwann merken, dass sie an ihren Ausgangspunkt zurückgekommen ist. Sie ginge immer geradeaus und lief dennoch (ohne sich dessen bewusst zu sein) einen gekrümmten Weg. Über diesen Vergleich kann man sich den Krümmungsradius des 3-dimensionalen Universums vorstellbar machen.]

Die Gleichungen zur Struktur und Expansion des Universums führen zu einer grafischen Darstellung der Expansion (Bild unten). Die dabei wichtigen Parameter sind:
R(t), der Krümmungsradius des Universums, der selbstverständlich zeitabhängig ist;
k, das Vorzeichen der Raumkrümmung, mit: k=-1, hyperbolischer Raum, der Raum ist ``offen''; oder k=0, euklidischer Raum; oder k=+1, sphärischer Raum, der Raum ist ``geschlossen'';
d(t), die mittlere Materiedichte des Universums. Hier wird die sogenannte kritische Dichte, d_crit(t), definiert; es ist die mittlere Dichte des Universums, falls k=0 zutrifft. Die bisher aus bekannten Objekten dokumentierbare Materiedichte ist nahezu einen Faktor 100 kleiner als die `kritische Dichte'!
H(t), die Hubble-Funktion, die die Art der Expansion beschreibt. Dabei ist H₀ (für Zeit t = heute) die Hubble-Konstante für die Expansion des Universums Hier und Heute. Nach heutiger Erkenntnis hat sie einen Wert zwischen 50 und 75 km/s pro Megaparsec Entfernung;
q(t), der Abbremsungsparameter, beschreibt wie die Expansion des Universums durch die Schwerkraft verzögert wird. Der zugelassene Wertebereich von q hängt mit der Wahl der Geometrie des Universums (Wert von k) zusammen.

Bei k=+1 ist der Raum geschlossen, die mittlere Materiedichte ist grösser als die kritische, und q grösser als 0.5; d.h., die Expansion des Universums wird derart verzögert, dass es zu einem Halt und anschliessend einer Schrumpfung kommt und das Universum wieder zusammenfällt.
Bei k=-1 ist der Raum offen, die mittlere Materiedichte wäre kleiner als die kritische, und q kleiner als 0.5; d.h., die Expansion des Universums wird ewig fortgesetzt.
Bei k=0 hat man den Grenzfall mit q=0.5, das Universum expandiert zwar immer weiter, aber immer langsamer.

Welcher der drei Fälle das Verhalten unseres expandierenden Universums am Besten wiedergibt, muss an Hand von Beobachtungen dokumentiert werden. Es gibt Überlegungen, die zum Ausschluss gewisser Modelle führen. 1) Eine abbremsende Expansion (k=+1 und q grösser als 0.5) und das spätere Zusammenziehen muss bedeuten, dass das Universum höchstens etwa 14 Milliarden Jahre alt wäre (für eine Hubble-Konstante von 50 km/s /Megaparsec). Dies ist weniger als das Alter der ältesten uns bekannten Sterne! Auch müsste die mittlere Materiedichte in diesem Fall grösser als die kritische Dichte sein (und es gibt schon so wenig Materie). 2) Auf ewig expandieren (k=-1 und q kleiner als 0.5) bedeutet ein relativ grosses Alter des Universums. Es bedeutet auch, dass das Universum immer kälter wird. 3) Da sowohl bei den Lösungen 1) als 2) Probleme auftauchen, besteht eine gewisse Präferenz für das Modell mit k=0, q=0.5 und die kritische Dichte als mittlere Materiedichte. Dazu kommt, dass dieses Modell genau den Grenzfall zwischen den anderen darstellt.

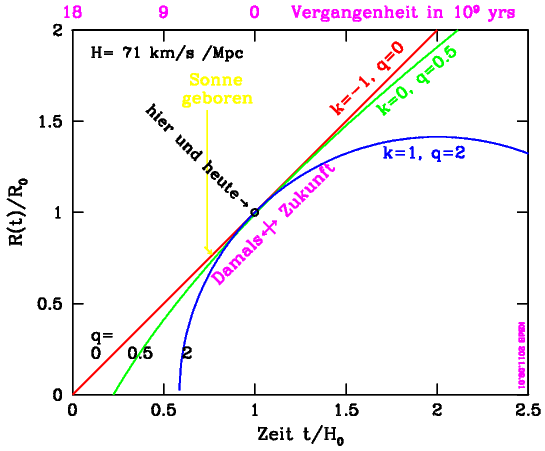
Das Verhalten des Universums in Bezug auf die Werte der relevanten Parameter ist in der Grafik zusammengefasst.

Die Modelle für Struktur und Entwicklung des Universums liefern eine Grafik, die die Expansion des Universums zeigt. Die Expansionsrate für das Universum "Hier und Heute" ist in allen Modellen selbstverständlich gleich H0. Die Grenzfälle unter den Modellen sind die mit q=0 (offen) und mit q=0.5 (Dichte genau gleich der kritischen Dichte). Modelle mit q grösser als 0.5 beschreiben geschlossene Universen, sie fallen in sich zurück, erfordern aber ein junges Alter des Universums in Widerspruch zum Alter der ältesten bekannten Sterne. Die Altersangabe am oberen Rand (in Einheiten von Milliarden Jahren) trifft zu für eine Hubble-Konstante mit Wert H0 = 71 km/s pro Megaparsec. Im favorisierten Modell mit q=0.5 wird viel Dunkle Materie gebraucht. [Bild von einem der Aktualität entsprechenden ersetzt am 2011.09.01]

Im Universum mit k=0 muss die mittlere Materiedichte gleich der kritischen Dichte sein. Die kritische Dichte ist, laut den Gleichungen zum Modell, zu finden aus
        d_crit(t) = 3 H(t)² / 8 pi G
mit der Konstante der Schwerkraft G. Die aktuelle mittlere Materiedichte wird aus den uns bekannten Masseanteilen unter Berücksichtigung der grossen Zwischenräume zwischen den Galaxien und den Galaxienhaufen berechnet. So findet man, dass die aktuelle Dichte der sichtbaren Materie nahezu nahezu einen Faktor 100 geringer ist als die kritische Dichte! Daraus leitet man die kosmologische Notwendigkeit für Dunkle Materie ab (für neuere Entwicklungen zur Theorie, siehe Kap. 5: DM oder kein DM?). Der Bedarf an DM ist hier aber etwa einen Faktor 10 grösser als bei dem Bedarf zur Erklärung der Rotationskurven und der Masse in Galaxienhaufen.

Ein weiterer Grund für DM ergibt sich aus der Betrachtung der kosmischen Hintergrundstrahlung. Nach dem Urknall kühlte das heisse homogene Universum herunter, und der Überrest dieser heissen Strahlung ist noch als Hintergrundstrahlung mit effektiv 3 Grad Kelvin im fern-infraroten Teil des Spektrums zu sehen. Dennoch bildeten sich Inhomogenitäten in der Dichte, die später zur Bildung von Galaxienhaufen mit den Galaxien darin führten. Beim Herunterkühlen werden Strahlung und Materie `entkoppelt', dass heisst, Strahlung und Materie benehmen sich von da an unabhängig. Schon vorhandene Inhomogenitäten sollten daher als Inhomogenitäten in der heute beobachtbaren Hintergrundstrahlung sichtbar sein. Die Inhomogenitäten sind aber gering, was nur verständlich ist, wenn die Materiedichte hoch war. Daraus ergibt sich ein grosser Bedarf an DM!

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

4. Hypothesen zur Natur der Dunklen Materie

Es gibt drei Richtungen, in der nach der Lösung des Problems der DM gesucht wird:

      1) Gibt es `normale' Materie, die das Problem löst?

      2) Gibt es `exotische' Materie, die das Problem löst?

      3) Sind die Gesetze zur Schwerkraft nach Newton und Einstein unvollständig?

Die Möglichkeit der normalen, baryonischen Materie wird dabei am ausführlichsten besprochen, da wir über normale Materie am besten Bescheid wissen.

zu 2) Nicht baryonische Materie
Es wurde eine Vielfalt an Elementarteilchen zur Erklärung der DM vorgeschlagen. Sie reicht von `normalen' bis hin zu exotischen Elementarteilchen. Meistens werden dann folgende genannt: Axionen, Neutrinos, Photinos, Monopole, WIMPs (weakly interacting massive particles), Planck Relikte. Eine eingehende Besprechung muss von Experten auf diesem Gebiet formuliert werden. Es sei auf das Thema Teilchenphysik hingewiesen.

Die Neutrinos gehören auch der nicht-baryonischen Kategorie an. Sie sind die einzigen Kandidaten, deren Existenz bewiesen ist. Neutrinos entstehen bei Kernfusionsprozessen. So sendet z.B. die Sonne einen Strom an Neutrinos aus, und auch in Supernova-Explosionen werden sie freigesetzt (siehe SN 1987A in der LMC). Sie haben eine sehr geringe Wechselwirkung mit anderer Materie. Aus gegenwärtiger Forschung an Neutrinos ergibt sich, dass deren Masse wohl zu klein ist, um die geforderte Menge an DM erklären zu können.

zu 3) Anpassung der Gravitationstheorie
Die Menge der geforderten DM führt über Modelle zu einer Abschätzung der Raumdichte der DM in Galaxien. Die DM befindet sich wohl vorwiegend im sichtbaren Bereich der Galaxien und ist offenbar mit der Dichte der sichtbaren Materie korreliert. Die Raumdichte der DM benimmt sich in Galaxien etwa proportional zu r^-2.

Die Gesetze der Gravitation zeigen, dass die Anziehungskraft zweier Objekte proportional zu r^-2 ist. Eine stärkere Gravitation würde folgen, wenn der Exponent nicht den exakten Wert 2 hat, sondern etwas kleiner wäre (dies bedeutet eine Kraft, die über grössere Entfernungen stärker ist als bei Newton). Über solche Änderungen der Gravitationsgesetze wird nachgedacht. Die Änderung hätte aber weitreichende Konsequenzen, z.B. für die Struktur und Entwicklung der Sterne, oder aber auch für die Modelle für die Struktur des ganzen Universums. Da die Gravitationsgesetze auf Newton zurückgehen, werden Theorien mit geänderten Gravitationsgesetzen dem Forschungsgebiet der MOdified Newtonian Dynamics (MOND) zugeordnet.

zu 1) Normale, baryonische Materie
Hier handelt es sich um `normale' Materie, die eben `normale' Objekte bilden kann.

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

`Normale' Objekte

Ist es nicht doch möglich, die benötigte DM in sehr schwer beobachtbaren aber dennoch normalen Objekten zu finden? Normale Objekte sind solche, deren Art uns bekannt ist, d.h. alle Art Objekte, die mit Sternen und Sternentwicklung zu tun haben, oder eben kalte Objekte wie Planeten oder kleine, feste Körper. Deswegen nun erst etwas über Sternentwicklung, sowie über die Frage wo DM am besten versteckt werden kann. Anschliessend werden 8 Objekttypen besprochen.

Kurzbeschreibung der Sternentwicklung

Welche Objekte kämen nun in Frage? Wenn es um Sterne geht, muss bekannt sein wie Sterne sich entwickeln (siehe Aufsatz Von der Geburt bis zum Tod der Sterne). Sterne die ihr Leben mit etwa 1 Sonnenmasse anfangen, haben eine Lebenserwartung von etwa 10 Milliarden Jahren. Sie werden zu Roten Riesen, verlieren dann die Masse ihrer Hülle, schrumpfen, werden an der Oberfläche heiss, und kühlen danach herunter zu Weissen Zwergen. Sterne die mit viel Masse anfangen, gehen verschwenderisch mit ihrem Material um (es gibt eben die Beziehung Lebenserwartung proportional zu etwa 1/M²), so dass ein Stern mit anfänglich 30 Sonnenmassen insgesamt nur 10 Millionen Jahre zu leben hat. Nach verschiedenen Zwischenstufen der Sternentwicklung explodiert er als Supernova, übrig bleibt ein Neutronenstern als Restobjekt.

Wie könnte DM in baryonischer Form am besten versteckt sein?

Da eine Erklärung für dunkle Materie gefunden werden muss, dürfen die Objekte von sich aus kaum Licht produzieren. Damit sind sofort die helleren und deswegen massereicheren Sterne ausgeschlossen.

Normalerweise sind Objekte in Galaxien kugelförmig. Diese Form umfasst das grösste Volumen bei gegebener Oberfläche. Eine Kugel mit Radius r und Materie mit Dichte d habe eine Masse m. Sie bedecke von uns aus gesehen eine Fläche mit einem Querschnitt q:
        m = d (4pi/3) r³         und         q = pi r²
Die Gesamtzahl N der benötigten DM-Teilchen findet man aus der abgeschätzten erforderlichen Gesamtmasse M der DM und der Masse eines Teilchens. Die Summe der Querschnitte aller dieser N Teilchen ist auch von Bedeutung, da der Gesamtquerschnitt Q so klein sein muss, dass die weite Ferne des Universums nicht abgedeckt wird. Die Gleichungen lauten:
          N = M / m         und         Q = N q
Daraus ergibt sich eine Relation zwischen der Gesamtmasse der DM und dem Gesamtquerschnitt:
        M = 4/3 d r Q
Da M gegeben ist und Q möglichst klein sein soll (wir können ja bis in grösste Entfernung schauen), sind unter normale Objekte solche mit grossem d (führt zu grossem M und kleinem Q) am besten geeignet, die DM zu beherbergen oder zu verstecken.

1): Sichtbare Sterne: M Zwerge

Bei Sternbildung entstehen auch Objekte mit weit weniger Masse als die Sonne, die man nach der äusseren Erscheinungsform (Spektrum) M-Sterne nennt. Die Masse eines Objekts muss allerdings grösser als 0.08 M(Sonne) sein, um zu einem normalen Stern zu werden. Es entstehen bevorzugt massearme Sterne, wie M Zwerge, und weit seltener massereiche. In allen normalen Sternen (also auch in M Zwergen) ist die Materiedichte d nicht sehr gross, die Gase im Inneren verhalten sich wie `ideale Gase'. Mit wenig Masse sind solche Sterne nicht leuchtkräftig und an der Oberfläche kühl. Letzteres bedeutet, dass sie fast nur im infraroten Bereich des Spektrums `gesehen' werden können. Messungen im nahen IR ergaben, dass die Zahl der beobachteten M Zwerge nicht gross genug ist, um die DM zu beherbergen.

2): Sichtbare Sterne: Weisse Zwerge

Weisse Zwerge (white dwarfs, WDs) sind Sterne des Endstadiums der Entwicklung massearmer Sterne. Sie haben eine Masse von etwa 0.5 bis 1.2 Sonnenmassen. Die Kernmaterie ist entartet, daher kompakt. Die Oberfläche solcher Sterne kühlt aus, und solche kalten WDs sind sehr lichtschwach. Da sie aus massearmen Sternen stammen, wird dieses Stadium erst nach langer Zeit erreicht (mehr als einige Milliarden Jahre nach der Entstehung der Galaxis). Das Universum (Alter etwa 15 Milliarden Jahre) hat vermutlich nicht genug Zeit gehabt, die Menge an WDs zu erzeugen, die ausreicht um die DM zu erklären.
NEUERDINGS haben Astronomen grössere Zahlen kühle WDs (allerdings mit blauer Farbe) gefunden (siehe Science, Vol 291, p. 2293, 23 March 2001; oder die Veröffentlichung von Oppenheimer et al bei "Sciencexpress").

3): Unsichtbare Sterne: Neutronensterne

Am Ende der Entwicklung eines massereichen Sterns bleibt ein Neutronenstern (NS). Diese haben eine Masse von etwa 1.4 M(Sonne) und sind sehr kompakt (die Dichte des Materials ist die der Neutronen, etwa 2 10¹⁸ kg/m³). Hier wäre daher d sehr gross, und mit kleinem r wäre auch Q klein. Für die Argumente gegen NS zur Erklärung der DM siehe bei `Schwarze Löcher'.

4): Unsichtbare Sterne: Schwarze Löcher

Da die meisten Sterne als Doppelsystem existieren, wird in Doppelsystemen oft Masse vom einen Stern auf den anderen übertragen. Daher kann in massereichen Systemen der massereichere Stern, der als erster zur Supernova und dann zu einem NS wird, an Masse zunehmen und dann ab 2.2 M(Sonne) zum Schwarzen Loch (Black Hole, BH) werden. Die Materiedichte d ist noch höher als bei NS, der Radius r ist noch kleiner.

Da Neutronensterne und Schwarze Löcher so kompakt sind, könnte man die DM gut in ihnen verstecken. Die notwendige Zahl dieser Objekte wäre dann aber so gross, dass es Probleme mit der Entwicklung der Galaxis gäbe: Massereiche Sterne produzieren über Kernfusion schwere Elemente in deren Zentralbereich. Bei einer Supernova-Explosion wird eine erhebliche Menge dieses `angereicherten' Materials an den interstellaren Raum zurückgegeben. Dadurch wird die Galaxis mit schweren Elementen angereichert, es gibt eine `chemische' Entwicklung der Galaxis. Da nach dem Urknall zunächst keine schweren Elemente vorhanden sind, kann man abschätzen, wieviel an schweren Elemente über die Prozesse in massereichen Sternen seither erzeugt worden sein muss. Die heute beobachtete Menge an schweren Elementen deutet auf eine Gesamtzahl der Supernova-Explosionen, die weit kleiner ist als die Zahl der zur Erklärung der Dunklen Materie notwendigen NS und BH. Daher kommen diese Objekte doch nicht im Frage, um die DM zu verstecken.

5): Fast unsichtbares: Braune Zwerge

Wenn sich Sterne bilden, entstehen bevorzugt Sterne geringer Masse. Die Verteilung über Massenintervalle nennt man die Massenfunktion. Sterne in statu nascendi, denen es nicht gelingt, mehr als 0.08 Sonnenmassen anzusammeln, werden keine Kernfusion (oder nur ganz wenig aus Deuterium) in ihrem Zentrum haben, werden daher nicht (oder kaum) zum `Stern'. Sie strahlen im Infrarot auch Energie aus der Kontraktion ab. Solche Objekte nennt man `Braune Zwerge'. Die Materiedichte d ist aber nicht sehr gross. Sie sind allerdings geeignete Kandidaten für die DM, da sie einiges an Masse enthalten, dennoch kaum Strahlung abgeben und daher nahezu unsichtbar sind. [ Neue Erkenntnisse zeigen, dass sie vielleicht 10% zu der Gesamtmasse an Baryonen beitragen. (2002.08.28)]

6): Sehr schwer sichtbares: Planeten

Planeten sind Objekte ohne innere Energiequelle. Es gibt Planeten, die eine feste Oberfläche haben wie die Erde und solche, die gasförmig sind wie Jupiter. Die Masse liegt deutlich unter einem Prozent der Sonnenmasse. Sie sind schwer zu entdecken und man braucht sehr viele, eigentlich zu viele Planeten, um die DM zu erklären. Zu viele Planeten im Raum würde zu vielen Kollisionen mit anderen Objekten führen, sie würden dadurch auseinanderfallen und zu kleineren Objekten werden, oder aber sie stürzen in Sterne hinein (wie Kometen es tun).

7): Selten sichtbares: Kometen

Kometen sind kleine Objekte mit geringer Materiedichte. Man braucht viel zu viele Kometen, um die DM zu erklären, Q wäre dann viel zu gross. Dazu würden sie untereinander oder mit anderen Objekten kollidieren (z.B. in die Sonne stürzen). Kometen können die DM-Problematik nicht lösen.

8): Unsichtbares: Schneebälle

Bei den angedachten Schneebällen gilt die Problematik wie bei Kometen noch stärker: zu geringe Dichte, viel zu grosses N, zu grosses Q, zu viele Kollisionen.

Zusammenfassung

Fazit: um die DM in normalen Objekten zu verstecken, sind die meisten Arten dieser Objekte nicht geeignet.

• Massearme Objekte geringer Dichte führen zu viel zu grossem Q.
• Die massereichen NS und BH führen zu einem Widerspruch mit der chemischen Entwicklung der Galaxis.
• M Zwerge würden insgesamt mehr Strahlung produzieren, als mit den Beobachtungen verträglich ist.
• Braune Zwerge aber wären geeignet: sie sind dunkel, nicht zu gross und enthalten je mehr als etwa 0.01 M(Sonne). Sie könnten die für die Galaxis notwendige DM enthalten.

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

5. DM oder keine DM?

Die Argumente für eine zusätzliche dunkle Massenkomponente in Galaxien und Galaxienhaufen sind stark. Die Argumente für DM aus der Kosmologie sind stark je nach favorisiertem Model für das Universum. Bis jetzt ist noch keine `normale' Objektsorte definiert, die die DM beherbergen kann, obwohl Braune Zwerge einen erheblichen Anteil der in Galaxien notwendigen DM erklären könnten. Dennoch bleibt die Frage: Ist die DM reell oder liegt ein Fehler in den Theorien vor?

Das Argument für DM aus der Kosmologie kann sehr deutlich abgeschwächt werden. Dies hängt mit der sogenannten kosmologischen Konstante zusammen. Die Gleichungen zur Beschreibung der Struktur des Universums enthalten nach Einstein auch ein Glied, in der ein Parameter `Lambda' steckt. Dieser Parameter stellt die `Energiedichte des Vakuums' dar. Sie bewirkt, dass das Universum gut expandieren kann, etwa wie eine Beschleunigung der Expansion.

In den theoretischen Überlegungen des mittleren bis späten 20.Jh. wurde diese kosmologische Konstante aus Bequemlichkeitsgründen (aber auch da Einstein sie öffentlich zurückgezogen hatte) gleich 0 gesetzt. Inzwischen gibt es eine Reihe Hinweise dafür, dass `Lambda' nicht gleich 0 ist. Es bedeutet gleichzeitig, dass der Bedarf an DM dadurch geringer wird. Einerseits könnte man sich gut vorstellen, dass das Universum mit einer normalen Materiedichte auskommt, dafür aber die kosmologische Konstante ziemlich bedeutsam sein muss. Dementsprechend müssen die Modelle für die Entwicklung des Universums ganz anders aufgezogen werden. Dies wird heutzutage (etwas zögerlich) weiter erforscht. Andererseits wäre dies in Widerspruch zu den Hinweisen für DM aus der Homogenität der kosmischen Hintergrundstrahlung. Die dafür notwendige DM kann dann aber nicht aus `normalen' Teilchen zusammengesetzt sein, muss nicht baryonischer Art sein.

Die in Verbindung mit der DM benutzten Parameter werden immer noch bezogen auf die kritische Dichte. Dabei ist "Omega" der auf dem Wert 1 umnormierte kritische Dichte. Man deutet die Menge der notwendigen mittleren Materiedichte mit dem Parameter "Omega"M an, der das Verhältnis der "beobachteten" zur kritischen Dichte darstellt. Ebenfalls gibt es den Parameter "Omega"Lambda, der die Bedeutung der kosmologischen Konstante "Lambda" in Verbindung zur kritischen Dichte setzt.
(2004.08.24: Nach dem WMAP-Experiment ist "Omega"=1.02, "Omega"M=0.3, "Omega"Lambda=0.7, und weitere Komponentnen (wie Strahlung) tragen nur vernachlässigbar bei.)

Wenn weitere Beobachtungen über die Art der Expansion des Universums bestätigen würden, dass die kosmologische Konstante eine grosse Bedeutung hat, dann gibt es daraus weniger Notwendigkeit für grosse Mengen an `kosmologischer' DM, aus der kosmischen Hintergrundstrahlung aber immer noch. Für die Problematik der Rotationskurven der Galaxien und die der Galaxienhaufen gäbe es die bei `Normale Objekte' diskutierte Lösung.

Links zu   Top   1. Strukt. & Bew.   2. Weitere Arg. f. DM   3. Kosmol. & DM   4. Hypoth. zur DM Natur   5. DM oder keine DM?

Text des Vortrags gehalten am 23 Februar 2000 in Bonn in der Vortragsreihe Physik heute