The existence of Dark Matter
is still one of the big challenges in modern astrophysics. Since its
early
inference Jan Oort, who found the stars in the local neighbourhood to
be moving
somewhat fast as compared to the gravitational potential they should
give rise
to, and by Fritz Zwicky in 1933 who found that galaxies in clusters are
apparently moving too fast, this phenomenon has accompanied astronomy
and astrophysics
ever since. The pioneering work by Vera
Rubin and her collaborators on optical (Hα) galaxy rotation curves
proved
the prevailance of Dark Matter in galaxies, which was later on followed
up by
the radio (HI) observations, first systematically conducted by Albert
Bosma. It was in the mid 90’s when the study of Dark Matter
experienced
kind of a revival: with the advent of numerical simulations of
structure
formation with Cold Dark Matter (CDM) à la Navarro,
Frenk & White (1996) it became possible to juxtapose
observations and
theory for a critical evaluation – and this is still going on. When
fitting an
analytical density profile to the resulting density distributions,
these
cosmological simulations predict a density profile (the so-called “NFW
profile”)
of the form

Here, ρc is the
critical density, rs the characteristic radius, and δc
is
a dimensionless constant. On large scales (clusters, superclusters,
cosmological filaments), CDM simulations have proven very successful,
while on
smaller (galaxy) scales, they were faced with a number of problems,
namely
- The cusp problem: the density profiles of simulated galaxies possess a central cusp, according tothe above law, while this is not observed in many galaxies, in particular in those with low masses (so-called dwarf galaxies).
The angular momentum problem: simulated galaxies come out too small, or have too little angular momentum.
The satellite problem: simulated DM halos possess a host of substructure. However, one observes but few satellite galaxies around larger ones (e.g our Milky Way).
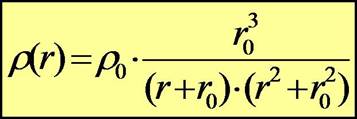
The solution of these problems
has been sought for in
observations, which always suffer from artefacts. They could naturally
also be
due to the (unknown) properties of the Dark Matter (e.g. finite
cross-sections
to interactions with baryons, self-annihilation, etc.). It is at this
point
where the whole subject becomes (at last) exciting: if we are able to
map the
density profiles of the dark halos of galaxies with sufficient
precision, we
should be able to contribute significantly to disclose the nature of
Dark
Matter! This is one of the goals of our investigations. In an ongoing
study of galaxy kinematics using HI and
Hα rotation curves, we
aim at exploring the central density distributions of the dark halos.
We need
sensitive measurements of the 21-cm HI line, which we achieve using the
WSRT and the VLA in the northern and the ATCA in the southern
sky. From
the observed HI data cubes, i.e. the measured brightness temperature as
a
function of position and velocity, Tb(ξ,η,v),
the rotation curve is derived and may be combined with optical (Hα) or
interferometric CO measurements to achieve higher spatial resolution in
the
central regions. The observed rotation curve delivers a mass
decomposition via

In case of a spheroidal
distribution of the Dark
Matter, the density profile of the dark halo may be obtained via

where the Poisson takes its most
simple form. Our
results so far favour pseudo-isothermal dark halos, rather than
distributions
predicted by CDM simulations. The example below shows measured rotation
curves
(Ha and HI combined)
of three low-luminosity galaxies. In the upper row, Burkert halos have
been
fitted, while the lower one exhibits fits top NFW density profiles. The
individual lines indicate the total rotational velocity (solid), the
dark halo
(long-dashed), the stellar (dotted), and the gaseous (short-dashed)
component. It
is obvious that the former yield a better fit. In particular, the NFW
profiles
require unrealistic mass-to-light ratios (taken from Gentile
et al. 2004).

In the course of our studies, we
also aimed at
studying the outer peripheries of galaxies. Whatever the amount and
property of
the Dark Matter, galaxies should eventually exhibit a decline in their
rotation
curves. Alas, such a decline has not been encountered hitherto, in
spite of
sporadic claims. In order to derive reliable rotation curves, it is
indispensable to deproject the observed velocities. This is an easy
thing to do
in case of flat disks; all one needs is the position angle and
inclination of
the galaxy under study. However, nature is more complicated. When
studying
galaxies out to large distances using the 21-cm line of neutral
hydrogen one
almost invariably encounters deviations from flat disks, such as warps
or
lopsidedness. A prominent example of such a warp is visible in outer HI
disk of
the spiral galaxy NGC5055, as shown in the following picture (Battaglia
et al. 2006; see also Tom
Osterloo’s web pages for spectacular examples of the extent of
gaseous
disks of galaxies). Even without the illustrating sketch, the warp is
readily
seen.

Our newly developed code tirific
(Gyula
Józsa) permits to investigate galaxies with warps or other
deviations from
a simple flat disk. This technique allows a reliable parametrization of
the
warp geometries by directly using the HI data cubes. We know three
types of
warps, which are illustrated below.



Our tools allows us to find the
rules which warps
'obey to'. Warps usually commence at the galacto-centric radius where
the
stellar disk fades away. This is also coincident with a sudden decrease
of the
surface brightness of the HI emission, or mass density of the gaseous
disk.
Most notably, warps also occur in isolated galaxies, so that in these
cases
they cannot be tidally induced by companion galaxies. Our analyses of
warps
permit to disentangle seemingly complicated cases: strong warps with
simple
kinematics may mimic complex systems, such as for instance polar-ring
galaxies.
A possible and attractive explanation of the warp phenomenon is that we
are
dealing with two distinct dynamical systems, an inner disk governed by
the
gravitational potential of the baryons (which dominate there), and an
outer
disk obeying to the potential of a (flattened) dark halo. If the two
systems
have some misalignment of their angular momenta, this gives
immediate
rise to a warp. We have recently illustrated our findings and
conjectures in popular
scientific form (Klein et al. 2005). Our
relevant
publications in professional journals may be found here.
Some examples of warp analyses are shown below. The three rows show
three
galaxies each, viz. NGC2541, UGC3580 and NGC5204 (LTR). In the first
row their
HI distributions (contours) are superimposed onto optical (i'-band)
images.
This is followed by the kinematic and structural parameters. In the
third row,
we finally display an “opaque view” of their gaseous disks, resulting
from the
model cubes.



The close agreement of our
models and observations may
be demonstrated by the following movie, which shows the observed and
fitted
model data cube of NGC5204; one should watch this movie several times.
The HI
column density, represented in grey-scale, has iso-velocity contours
superimposed. As the movie proceeds, one sees contours of HI brightness
as a
function of velocity (we are passing through the HI cube). Red contours
represent the observations, while blue ones reflect the model cube. The
correspondence of the two is obvious. The blue/red lines with crosses
represent
the line of nodes and its normal (kinematic major and minor axes).

We had furthermore started
collaboration with both,
theoretical astrophysics (numerical simulations, Andi Burkert) and
particle
physics (theoretical particle physics, Manuel Drees).
The
goal of this project was to mutually deliver pertinent information that
can be
used to constrain the parameter space of the Dark Matter candidates. An
excellent and comprehensive review of the particle candidates of Dark
Matter
was published by Bertone,
Hooper & Silk (2005). Such a collaboration among physicists and astrophysicists is particularly
useful in
view of LHC
at CERN. This accelerator will doubtlessly contribute to this field by
producing
candidate particles for Dark Matter. Furthermore, there are quite a few
experiments (being) set up to directly detect Dark-Matter particles via
recoil,
such as CDMS or XENON. Other
experiments
take an indirect route, by observing secondary (decay) products such as
neutrinos (ANTARES, ICECUBE), or Čerenkov radiation
produced by
γ-rays as they pass through the earth’s atmosphere (e.g. H.E.S.S.).
Our research has seen financial
support by the Deutsche
Forschungsgemeinschaft.





