



Next: Multi-frequency deconvolution --
Up: Deconvolution with maximum
Previous: Theory
Maximum entropy algorithms tend to be less robust and harder to drive than
CLEAN algorithms. The quality of the maximum entropy solution can depend
very strongly on the rms and flux parameters -- these parameters
should be set with some care, or some experimentation may be necessary.
Various parameters to the task maxen
are described below:
- map, beam: As with CLEAN, you give task maxen
a dirty
image and a dirty beam.
- default: You also have the option of supplying a default
image. The default image (
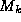 in the equations above) is some
estimate of what the algorithm should tend towards. It could be some
a priori model or low-resolution image of the source. The default
default (sic) image is a uniform image. The units of the
in the equations above) is some
estimate of what the algorithm should tend towards. It could be some
a priori model or low-resolution image of the source. The default
default (sic) image is a uniform image. The units of the default
image are not too important, though it should be positive valued if the
Gull and Skilling entropy measure is used. The default image
must align exactly with the region being deconvolved. That is, it
must have the same pixel increments, and same size as the bounding box
of the selected region.
- model: The
model is some initial estimate of the deconvolved
image (units of Jy/pixel). Like the default image, the model
must align exactly with the region being deconvolved. In principle,
the model image is simply a way to kick start maxen
towards the
correct solution. In principle it should not affect convergence to the final
solution or its quality -- it should just speed up the process. In practice,
a good initial model can sometimes help.
- region: As with CLEAN, this gives the region in the dirty image
which contains all the source emission, and much the same can be restated
here about setting the parameter. In particular, you can
deconvolve an area no more than a quarter the area of the beam (but see
options=pad if you fail to heed this advice.
- measure: This determines the entropy measure used; specify either
gull or cornwell (these are the
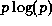 and
and 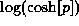 forms,
respectively). The default is to use the Gull form, but if deconvolving
Q
, U
or V
images, the Cornwell form may be useful.
forms,
respectively). The default is to use the Gull form, but if deconvolving
Q
, U
or V
images, the Cornwell form may be useful.
- out: This gives the name of the output image, which has units
of Jy/pixel. This is the equivalent image to clean
's CLEAN component
image. However, unlike CLEAN, maximum entropy techniques tend to be more
conservative in their extrapolation of high spatial frequencies, and so
this output is more commonly viewed and used as a final image than
the CLEAN component image would be. However it is just as valid an
operation to pass this output from maxen
through restor
,
and so produce either a restored or a residual image. Those with some
courage may choose to look at the residual image. Unlike CLEAN, the
residuals tend to be strongly correlated with source structure.
- niters: Task maxen
uses an iterative algorithm to
arrive at its solution, and terminates when it believes it has
converged. The parameter
niters gives the maximum number of
iterations that maxen
will attempt before giving up if it does
not converge. For low dynamic-range images, 10 iterations are usually
sufficient. Higher dynamic-ranges (greater than 1000) can require 30
iterations to converge. The default maximum number of iterations is 20.
- rms: This is a crucial parameter. It gives the rms noise in
Jy/beam. The rms noise value printed by invert
should be some
guide to setting this parameter, but see the caveats about this value
under invert
. An alternative way is to measure the rms in a
blank portion of the sky. If the beam has few sidelobes you will
probably be able to measure this directly from the dirty image.
Otherwise you would really need to CLEAN first! If
rms is too
large, the output image will be too smooth. If it is too small,
convergence will be prevented. A useful trick is to underestimate
rms and then stop after a few iterations, and then reset
rms to the level achieved up to that point. Do not leave
rms unset.
- flux: The
flux specifies how the zero-spacing flux density
is to be estimated. There are three modes of use. First, you specify a
known value which must be fitted to within 5%. Second, if you have no
idea what the zero-spacing flux density is, then leave flux unset;
maxen
will attempt to estimate it. Third, if you have a rough
idea (within a factor of 2, say) then set flux to the negative of
your guess. If at all possible, you should give some estimate of the
total flux density.
- q: This gives an estimate of the volume of the main lobe of the
dirty
beam in units of pixels. Typically it is 10 to 30, and the algorithm does
not depend critically on it. The default is determined from the data, and
generally will be adequate.
- options, as usual, gives several processing options. Possible
values are
- quiet, verbose:
- This controls the verbosity of maxen
's
messages.
- asym:
- Normally clean
assumes that the beam has a 180
degree rotational symmetry, which is the norm in radio interferometry.
Making such an assumption allows some optimisations. You should instruct
clean
if this is not the case, by using the asym switch.
- pad:
- Double the beam size by padding it with zeros. This will
give better stability with Clark and Steer modes if you are daring enough
to CLEAN an area which is more than a quarter of the beam area.





Next: Multi-frequency deconvolution --
Up: Deconvolution with maximum
Previous: Theory
Last generated by rsault@atnf.csiro.au on 16 Jan 1996
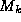 in the equations above) is some
estimate of what the algorithm should tend towards. It could be some
a priori model or low-resolution image of the source. The default
default (sic) image is a uniform image. The units of the
in the equations above) is some
estimate of what the algorithm should tend towards. It could be some
a priori model or low-resolution image of the source. The default
default (sic) image is a uniform image. The units of the 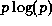 and
and 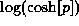 forms,
respectively). The default is to use the Gull form, but if deconvolving
Q
, U
or V
images, the Cornwell form may be useful.
forms,
respectively). The default is to use the Gull form, but if deconvolving
Q
, U
or V
images, the Cornwell form may be useful.
