



Next: Image Deconvolution
Up: Imaging
Previous: Weighting
Task invert
is a fairly conventional imaging program, which
produces a dirty image from a visibility dataset. It normally does this
using a grid-and-FFT approach, although there are switches to use a
direct Fourier transform and a median algorithm. Task invert
does not require the data to be sorted in any way.
Normally any calibration tables are applied
by invert
on-the-fly (although this can be turned off with the
nocal, nopol and nopass options). Both
continuum or spectral line observations are handled.
We describe the inputs to invert
. For MFS imaging, note
options=mfs (and options=sdb) options.
- vis gives the name of the input visibility datasets.
Several datasets can be given, as may be convenient when a source is
observed with multiple configurations or multiple frequencies.
The selected data are assumed to
be of the same object, with the same pointing centre. Additionally,
when making spectral line cubes, the number of channels derived from each
dataset must be the same (this restriction
does not apply for MFS images). Dataset names can include wildcards.
- map is the name of the output image dataset(s). When several Stokes
parameters are being imaged, you need to give one name for each Stokes
type. There is no default.
- beam is the name of the output beam dataset. The default is not
to create an output beam. If you wish to deconvolve, then you must
create an output beam. Note that invert
produces a single beam
which corresponds to all image planes and Stokes parameters.
- cell gives the image pixel size in arcseconds. Either one or two
values can be given. If only one value is given, the pixels are square. The
default is to choose a pixel size which samples the synthesised beam by
about a factor of 3 (i.e. the recommended sampling for deconvolution).
- imsize gives the size of the images in pixels. It need not
be a power of two. Generally the beam is also this size, but see
options=double below.
- line is the normal data linetype selection. The default linetype
is the first channel when performing normal imaging and all channels
when doing multi-frequency synthesis. Generally you should set this
parameter if you have more than one channel.
- select is the normal visibility data selection. The default is
to select all data.
- stokes gives the Stokes or polarisation types to be imaged.
Several values can be given, separated by commas. For example
stokes=i,q,u,v
will cause images of Stokes I
, Q
, U
and V
to be formed. Note
that there needs to be a corresponding output file (see map
above) for each Stokes parameter being imaged. The default Stokes parameter
to image is `ii', which images Stokes-I, and assumes that the source is
otherwise unpolarised.
- offset: This gives an offset, in arcseconds on the sky, to shift the image
centre away from phase centre. Positive values result in the
image centre being to the north and east of the observing centre. If one value
is given, both RA and DEC are shifted by this amount. If two values are given,
then they are the RA and DEC shifts. The default is no shift.
- options gives extra processing options. Several options can
be given (abbreviated to uniqueness), separated by commas. Possible
values are:
- mfs:
- This invokes multi-frequency synthesis imaging, as
described above. All selected channels and frequencies will be gridded
simultaneously to form a single output image.
- sdb:
-
This is used in MFS imaging to cause invert
to produce a spectral
dirty beam (this is stored as a second plane of the beam data-set).
The spectral dirty beam is used by the
deconvolution task mfclean
in determining the spectral index of the
image. Generally if you think you may use mfclean
to deconvolve
your image, then you should set options=sdb.
See the discussion of multi-frequency synthesis in Section 13.3
for more information.
- double:
- Normally invert
makes a beam which is the same
size as the image. However MIRIAD
's deconvolution tasks generally require
a beam which is four times the area than the region being deconvolved.
The double option causes invert
to produce a beam which is
twice the linear extent (four times the area) of the image. In this way,
you can request invert
to map just the region containing real
emission, plus a guard band (at least 5 pixels on each edge).
- systemp:
- See the description in the weighting section above.
- nocal:
- By default, invert
applies any gain
calibration to the data before imaging. The nocal option turns
off this step.
- nopass:
- By default, invert
applies any bandpass
calibration to the data before imaging. The nopass option turns
off this step.
- nopol:
- By default, invert
applies any polarisation
leakage correction to the data before imaging. The nopol option
turns off this step.
- mosaic:
- This invokes invert
's mosaic mode. See
Chapter 20 for more information.
- imaginary:
- This makes the `imaginary' image. This is
useful for non-Hermitian data (holography) or for investigating certain
instrumental errors.
- amplitude:
- Set the phase of each visibility to zero before
imaging.
- phase:
- Set the amplitude of each visibility to unity before imaging.
- mode: This determines the imaging algorithm to be used. Possible
values are fft (a conventional grid and FFT imaging algorithm),
dft (a direct Fourier transform approach) and median (a median
Fourier transform). The dft approach produces fewer artifacts in the resultant
images, but at substantial computational expense. The median approach os
more robust to bad data and sidelobes, but at an even more substantial
computational cost. The default mode is fft -- this should be used
on all but the smallest datasets and images.
- slop: The slop factor. This is used in specrtal-line
imaging. See Section 15.9 for more information.
Typical inputs to invert
for a continuum experiment are given below.

For a spectral line observation, typical inputs would be

invert
prints out a few numbers that may be of use -- the average
system temperature, average system gain and theoretical rms noise.
The theoretical rms noise is calculated assuming that the only source of
error is the system temperature of the front-end receiver. No account
is made of calibration errors, sidelobes or any other `instrumental'
effects. The calculation correctly accounts for the weighting scheme
used in the imaging process. This theoretical noise is the level you
can expect in a detection experiment (assuming no interference or
confusion), and it is the best one can hope for in high dynamic range
work (usually instrumental effects will limit you before the noise
in these sorts of experiments).
The noise calculation of invert
(and all other MIRIAD
tasks that
compute the variance of a correlation) is based on values of system
temperature, system gain, integration time and bandwidth stored in a dataset.
Unfortunately data loaded into MIRIAD
using fits
will have only nominal
system temperatures and system gains, and an educated guess is made for the
integration time. Data loaded
using MIRIAD
atlod
, the
system temperatures are those measured on-line, and the integration time
will be correct.
See Chapter 8 for a discussion of setting you dataset
up so that noise estimates are correct. The system gain, however, is still
a nominal figure. If system temperature, system gain or integration time
are incorrect by some factor, then the
theoretical rms noise will also be wrong by a factor.
There is another effect which will cause invert
's noise estimate
to be a factor of
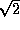 too pessimistic (i.e. the actual noise is a factor of
too pessimistic (i.e. the actual noise is a factor of 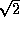 lower than the printed value). With the ATCA correlator in its
continuum (33 channel) mode, the channel bandwidth
is twice as large as the separation between channels ( i.e. the channels
are oversampled). Unfortunately invert
assumes that the
bandwidth is the same as the separation. This will only affect
you if you are imaging individual correlator channels (i.e. no frequency
averaging). It will not affect ``channel 0'' or multi-frequency synthesis
imaging.
lower than the printed value). With the ATCA correlator in its
continuum (33 channel) mode, the channel bandwidth
is twice as large as the separation between channels ( i.e. the channels
are oversampled). Unfortunately invert
assumes that the
bandwidth is the same as the separation. This will only affect
you if you are imaging individual correlator channels (i.e. no frequency
averaging). It will not affect ``channel 0'' or multi-frequency synthesis
imaging.




Next: Image Deconvolution
Up: Imaging
Previous: Weighting
Last generated by rsault@atnf.csiro.au on 16 Jan 1996



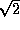 too pessimistic (i.e. the actual noise is a factor of
too pessimistic (i.e. the actual noise is a factor of 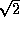 lower than the printed value). With the ATCA correlator in its
continuum (33 channel) mode, the channel bandwidth
is twice as large as the separation between channels ( i.e. the channels
are oversampled). Unfortunately invert
assumes that the
bandwidth is the same as the separation. This will only affect
you if you are imaging individual correlator channels (i.e. no frequency
averaging). It will not affect ``channel 0'' or multi-frequency synthesis
imaging.
lower than the printed value). With the ATCA correlator in its
continuum (33 channel) mode, the channel bandwidth
is twice as large as the separation between channels ( i.e. the channels
are oversampled). Unfortunately invert
assumes that the
bandwidth is the same as the separation. This will only affect
you if you are imaging individual correlator channels (i.e. no frequency
averaging). It will not affect ``channel 0'' or multi-frequency synthesis
imaging.