Lambda-CDM model
From Wikipedia, the free encyclopedia
| Physical cosmology | ||||||||
 |
||||||||
| Universe
· Big
Bang Age of the universe Timeline of the Big Bang Ultimate fate of the universe
|
||||||||
ΛCDM or Lambda-CDM is an abbreviation for Lambda-Cold Dark Matter. It is frequently referred to as the standard model of big bang cosmology, since it attempts to explain the existence and structure of the cosmic microwave background, the large scale structure of galaxy clusters and the distribution of hydrogen, helium, lithium, oxygen and also the accelerating expansion of the universe observed in the light from distant galaxies and supernovae. It is the simplest model that is in general agreement with observed phenomena.
Contents[hide] |
[edit] Overview
- All modern cosmological models are based on the cosmological principle that our observational location in the universe is in no way unusual or special: on a large enough scale, the universe looks the same in all directions (isotropy) and from every location (homogeneity).[1]
- The model includes an expansion of metric space that is well documented both as the red shift of prominent spectral absorption or emission lines in the light from distant galaxies and as the time dilation in the light decay of supernova luminosity curves. Both effects are attributed to a Doppler shift in electromagnetic radiation as it travels across expanding space. Paradoxically, while this expansion increases the distance between objects that are not under shared gravitational influence, it does not increase the size of the objects in space. It also allows far distant galaxies to recede from each other at speeds greater than the speed of light.
- The model assumes a "flat" spatial geometry, which means that the interior angles of a triangle defined by three beams of light will sum to 180°; space is defined by straight lines. (Alternative geometries include a spherical or "closed universe" in which the interior angles of a triangle would sum to more than 180°, and a hyperbolic or "open universe", in which the angles would sum to less than 180°.) The current values of key parameters imply that the universe is either flat or slightly open, the universe will expand forever, and the expansion is accelerating.
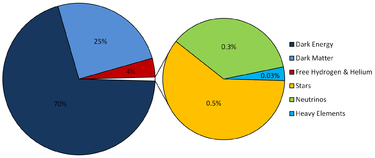
- Λ (Lambda) stands for the cosmological constant which is currently associated with a vacuum energy or dark energy inherent in empty space that explains the current accelerating expansion of space against the attractive (collapsing) effects of gravity. The cosmological constant is denoted as ΩΛ, which is interpreted as the fraction of the total mass-energy density of a flat universe that is attributed to dark energy. Currently, about 73% of the energy density of the present universe is estimated to be dark energy.
- Cold dark matter is a form of matter necessary to account for gravitational effects observed in very large scale structures (anomalies in the rotation of galaxies, the gravitational lensing of light by galaxy clusters, enhanced clustering of galaxies) that cannot be accounted for by the quantity of observed matter. Dark matter is described as being cold (i.e. its velocity is non-relativistic [far below the speed of light] at the epoch of radiation-matter equality), possibly non-baryonic (consisting of matter other than protons and neutrons), dissipationless (cannot cool by radiating photons) and collisionless (i.e., the dark matter particles interact with each other and other particles only through gravity). This component is currently estimated to constitute about 23% of the mass-energy density of the universe.
- The remaining 5% comprises all matter and energy observed as subatomic particles, chemical elements and electromagnetic radiation, the stuff of which visible planets, stars and galaxies are made.
- The model includes a single originating event, the "Big Bang" or initial singularity, which was not an explosion but the abrupt appearance of expanding space time containing radiation at temperatures of around 1015 K. This was immediately (within 10−29 second) followed by an exponential expansion of space by a scale multiplier of 1027 or more, known as cosmic inflation. The early universe remained hot (above 10,000 K) for several hundred thousand years, a state that is detectable as a residual cosmic microwave background or CMB, a very low energy radiation emanating from all parts of the sky. The "Big Bang" scenario, with cosmic inflation and standard particle physics, is the only current cosmological model consistent with the observed continuing expansion of space, the observed distribution of lighter elements (hydrogen, helium, lithium, oxygen) in the universe, and the spatial texture of minute irregularities (anisotropies) in the CMB radiation. Cosmic inflation is also necessary to address the "horizon problem" in the CMB. Indeed, it seems likely that the universe is larger than the observable particle horizon.
- The model uses the FLRW metric, the Friedmann equations and the cosmological equations of state to describe the observable universe from right after the inflationary epoch to present and future.
Historically, the dominant cosmological model previous to the now "standard model" was the Steady State theory, proposed independently in 1948 by H. Bondi & T. Gold and by Fred Hoyle. The universe in this model was flat, infinitely large, infinitely old (homogeneity and isotropy were extended in time as well as space) and was continuously creating matter to stabilize the mass energy density of expanding space. The ΛCDM model is remarkable in that it describes a dynamic, evolving universe, from the initial singularity, inflation, spatial expansion and the creation of all matter through the formation of more than 100 billion visible galaxies from a fixed quantity of matter. It foretells a future in which the metric expansion of space will carry all galaxies away from each other at speeds greater than light, and observers in each galaxy will see only their own galaxy in an otherwise empty universe.[2]
There is currently active research into many aspects of the ΛCDM model, which is very likely to change as new information becomes available. In particular, it is difficult to measure accurately the distance of very far galaxies or supernovae, so that distance related estimates (of stellar or galactic luminosities, or of key parameters such as the Hubble constant) are still uncertain. In addition, ΛCDM has no explicit physical theory for the origin or physical nature of dark matter or dark energy; the nearly scale-invariant spectrum of the CMB perturbations, and their image across the celestial sphere, are believed to result from very small thermal and acoustic irregularities at the point of recombination.
[edit] Parameters
The ΛCDM model is based on six parameters: physical baryon density, physical dark matter density, dark energy density, scalar spectral index, curvature fluctuation amplitude and reionization optical depth. From these the other model values, including the Hubble constant and age of the universe, can be derived.
Parameter values listed below are from the Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) temperature and polarization observations.[3] These include estimates based on data from Baryon Acoustic Oscillations and Type Ia supernova luminosity/time dilation measurements.[4] Implications of the data for cosmological models are discussed in Komatsu et al. [5] and Spergel et al.[6]
| Parameter | Value | Description |
|---|---|---|
| t0 | 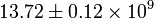 years years |
Age of the universe |
| H0 | 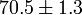 km s−1
Mpc−1 km s−1
Mpc−1 |
Hubble constant |
| Ωb | 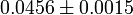 |
Baryon density |
| Ωc | 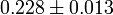 |
Dark matter density |
| ΩΛ | 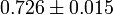 |
Dark energy density |
| Ωtot | 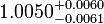 |
Total density |
| ΔR2 | 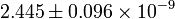 , k0
= 0.002Mpc−1 , k0
= 0.002Mpc−1 |
Curvature fluctuation amplitude |
| σ8 | 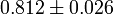 |
Fluctuation amplitude at 8h−1Mpc |
| ns | 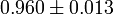 |
Scalar spectral index |
| z* | 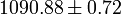 |
Redshift at decoupling |
| t* | 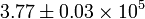 years years |
Age at decoupling |
| τ | 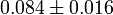 |
Reionization optical depth |
| zreion | 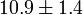 |
Redshift of reionization |
| treion | 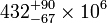 years years |
Age at reionization |
[edit] Extended models
Possible extensions of the simplest ΛCDM model are to allow quintessence rather than a cosmological constant. In this case, the equation of state of dark energy is allowed to differ from −1. Cosmic inflation predicts tensor fluctuations (gravitational waves). Their amplitude is parameterized by the tensor-to-scalar ratio, which is determined by the energy scale of inflation. Other modifications allow for spatial curvature or a running spectral index, which are generally viewed as inconsistent with cosmic inflation.
Allowing these parameters will generally increase the errors in the parameters quoted above, and may also shift the observed values somewhat.
| Parameter | Value | Description |
|---|---|---|
| w | 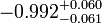 |
Equation of state |
| r | < 0.22, k0 = 0.002Mpc−1 (2σ) | Tensor-to-scalar ratio |
| α | 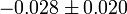 , k0
= 0.002Mpc−1 , k0
= 0.002Mpc−1 |
Running of the spectral index |
| Σmν | < 0.67 eV (2σ) | Neutrino mass |
Some researchers have suggested that there is a running spectral index, but no statistically significant study has revealed one. Theoretical expectations suggest that the tensor-to-scalar ratio r should be between 0 and 0.3, and the latest results are now within those limits.
[edit] See also
[edit] References
- ^ Andrew Liddle. An Introduction to Modern Cosmology (2nd ed.). London: Wiley, 2003.
- ^ Lawrence Krauss, "A Universe From Nothing". Presentation to the Atheist Alliance International, Burbank, CA 2009.
- ^ Table 7 of Hinshaw, G. et al. (WMAP Collaboration). (feb 2009). "Five-Year Wilkinson Microwave Anisotropy Probe Observations: Data Processing, Sky Maps, and Basic Results". The Astrophysical Journal Supplement 180: 225–245. doi:10.1088/0067-0049/180/2/225. arXiv:0803.0732. http://adsabs.harvard.edu/abs/2009ApJS..180..225H.
- ^ M. Kowalski et al. 2008 (Supernova Cosmology Project Collaboration). Improved Cosmological Constraints From New, Old and Combined Supernova Datasets.
- ^ E. Komatsu et al. 2009 (WMAP Collaboration). Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation.
- ^ D. N. Spergel et al. 2003 (WMAP collaboration). First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: determination of cosmological parameters, Astrophys. J. Suppl. 148 175 (2003).
- R. Rebolo et al. (VSA collaboration), Cosmological parameter estimation using Very Small Array data out to l=1500, Monthly Notices of the Royal Astronomical Society, Volume 353, Issue 3, pp. 747–759
- J. P. Ostriker and P. J. Steinhardt, Cosmic Concordance, arXiv:astro-ph/9505066.

