Gas Cooling
We use two cooling models in this work, denoted C1 and C2, which
differ in that C2 has significant cooling in the neutral gas. Our
first model, C1, contains four elements:
- Radiative losses due to recombining Hydrogen, calculated from
the non-equilibrium ion fraction and temperature in each cell
according to rates tabulated in Hummer (1994).
- Collisional ionisation of Hydrogen: this is relatively
unimportant because the rates are typically very low, but we
subtract the ionisation energy from the gas for each collisional
ionisation.
- Cooling due to heavy elements at high temperatures, using the
collisional ionisation equilibrium (CIE) cooling curve tabulated
in Sutherland (1993) and shown in their fig. 18. This provides
strong cooling in ionised gas with temperatures significantly larger
than
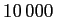 K.
Note that in CIE at
K.
Note that in CIE at 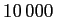 K, Hydrogen, Nitrogen
and Oxygen are neutral so this fitting function does not double
count the other terms in our cooling function, at least for the gas
temperatures encountered in our simulations.
K, Hydrogen, Nitrogen
and Oxygen are neutral so this fitting function does not double
count the other terms in our cooling function, at least for the gas
temperatures encountered in our simulations.
- A linear fit to collisionally excited emission from
photo-ionised Oxygen and Nitrogen (Osterbrock, 1989).
The last term is the most important for this work, since these ionic
species are the dominant coolants in H II regions and set the
equilibrium temperature in ionised gas of
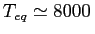 K.
In experiments with different cooling functions for ionised gas, we found
that the most important factor for the dynamical evolution of our
models was the equilibrium temperature. If the normalisation of the
cooling function is kept fixed at
K.
In experiments with different cooling functions for ionised gas, we found
that the most important factor for the dynamical evolution of our
models was the equilibrium temperature. If the normalisation of the
cooling function is kept fixed at 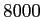 K, its slope has little
effect on the resulting dynamics so long as the slope is positive. If
we had strong shocks in the ionised gas this aspect of the cooling
function would have more influence, but the photo-ionised gas in our
simulations has a very narrow temperature range.
K, its slope has little
effect on the resulting dynamics so long as the slope is positive. If
we had strong shocks in the ionised gas this aspect of the cooling
function would have more influence, but the photo-ionised gas in our
simulations has a very narrow temperature range.
In this prescription the neutral atomic gas has no efficient cooling
avenue, and shocked neutral gas is typically at
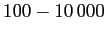 K.
This is undoubtedly a limitation in our modelling, but we do not yet
model the formation of molecules, or the formation/destruction of
dust, which are the primary neutral gas coolants in star forming
regions. To assess the effects of significant neutral gas cooling we
also use an alternate cooling function, C2, consisting of the
previous components in C1 plus additional exponential cooling
(Newton's Law) in neutral gas with a rate given by
K.
This is undoubtedly a limitation in our modelling, but we do not yet
model the formation of molecules, or the formation/destruction of
dust, which are the primary neutral gas coolants in star forming
regions. To assess the effects of significant neutral gas cooling we
also use an alternate cooling function, C2, consisting of the
previous components in C1 plus additional exponential cooling
(Newton's Law) in neutral gas with a rate given by
![$\displaystyle \dot{T} = \left[\frac{(1-x)^2}{10^N\mathrm{yrs}}\right] \left(T_{\infty}-T\right) \;,$](img46.png) |
(1.2) |
where 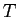 is gas temperature,
is gas temperature,
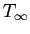 is the temperature to which
this cooling law relaxes at late times,
is the temperature to which
this cooling law relaxes at late times, 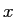 is the ionisation fraction
of the gas, and
is the ionisation fraction
of the gas, and  is a parameter specifying the chosen cooling
time-scale,
is a parameter specifying the chosen cooling
time-scale,
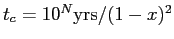 . The scaling with
. The scaling with 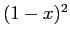 ensures only mostly neutral gas is affected. We set
ensures only mostly neutral gas is affected. We set
 K and
K and 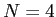 for the alternate models run in this
paper. This is not an extreme model either in terms of the
equilibrium temperature or the cooling time, having less cooling in
dense gas than e.g. Henney (2009). It is a very simple
prescription, with an effect which is intermediate between C1 and a
two-temperature isothermal
model (e.g. Lora, 2009; Gritschneder, 2009; Williams, 2001).
for the alternate models run in this
paper. This is not an extreme model either in terms of the
equilibrium temperature or the cooling time, having less cooling in
dense gas than e.g. Henney (2009). It is a very simple
prescription, with an effect which is intermediate between C1 and a
two-temperature isothermal
model (e.g. Lora, 2009; Gritschneder, 2009; Williams, 2001).
Jonathan Mackey
2010-01-07
![]() K.
This is undoubtedly a limitation in our modelling, but we do not yet
model the formation of molecules, or the formation/destruction of
dust, which are the primary neutral gas coolants in star forming
regions. To assess the effects of significant neutral gas cooling we
also use an alternate cooling function, C2, consisting of the
previous components in C1 plus additional exponential cooling
(Newton's Law) in neutral gas with a rate given by
K.
This is undoubtedly a limitation in our modelling, but we do not yet
model the formation of molecules, or the formation/destruction of
dust, which are the primary neutral gas coolants in star forming
regions. To assess the effects of significant neutral gas cooling we
also use an alternate cooling function, C2, consisting of the
previous components in C1 plus additional exponential cooling
(Newton's Law) in neutral gas with a rate given by
![$\displaystyle \dot{T} = \left[\frac{(1-x)^2}{10^N\mathrm{yrs}}\right] \left(T_{\infty}-T\right) \;,$](img46.png)