Rotationen im Sonnensystem, Lichtgeschwindigkeit, Entfernungen

Die Entwicklung der Ideen über die Struktur des Sonnensystems kann nur verstanden werden im Zusammenhang mit Ideen über Bewegung, Raum und Geschwindigkeit. Es erforderte genaue astronomische Messungen, elegante mathematische Darstellungen und physikalische Experimente, um die Dimensionen und Verhältnisse im Sonnensystem ordentlich zu beschreiben.

Inhalt: Dreht Erde um Sonne?   Entdeckung Jupiter Monde   Präzession   Foucaults Pendel   Lichtgeschwindigkeit   Jupitermonde und Lichtgeschwindigkeit   Aberration   Lichtgeschwindigkeit vom Experiment   Entfernung Erde-Sonne   Venustransit

1. Das Sonnensystem

a. Von Mesopotamiern und Griechen zu ersten Entdeckungen mit Teleskopen

In Mesopotamischen Zeiten waren die Beobachtungen des Sternhimmels so verfeinert, dass die Schleifen in den Bahnen der Planeten gut dokumentiert und die Rhythmen der Sonnen- und Mondfinsternisse gut bekannt waren. Dies führte zu einer ausgefeilten Rechenkunst. Sie benutzte das 12- und 60-zählige System, daher haben wir heute noch die dementsprechende Einteilung der Zeit und der Winkelkoordinatensysteme. Die Mesopotamier konnten Verfinsterungen im voraus berechnen, was zu großem Ansehen der "Astrologen" geführt hat.

Die Positionen der Sterne am Himmel erschienen ihnen als "fix". Auch die alten Griechen meinten, dass die Sterne fixiert an eine Himmelssphäre seien, da man bei geringer und ungleicher Entfernung eine (halb-)jährliche "parallaktische Bewegung" (siehe Abbildung unten) hätte sehen müssen.

Die Pythagoräer gaben vor 2500 Jahren einfachen Zahlen große Bedeutung. So waren die Planeten aufeinander folgenden Sphären zugeordnet, deren Zwischenräume durch einfache Zahlenverhältnisse angegeben werden konnten. Dies hänge womöglich mit den Schwingungszahlen einer Saite zusammen, und man sprach von der "Harmonie der Sphären". Vor 2300-2400 Jahren wurde dann vorgeschlagen, dass sich die Erde um die Sonne bewegt. Dennoch wurde diese Idee nicht weiter verfolgt, da eben die Bewegung nicht beweisbar war, und da Aristoteles argumentierte, dass Objekte aus Wasser und Erde zum Erdkörper wiederkehren und damit die Erde im Mittelpunkt des Planetensystems sein muss. Dies führte (Ptolemäus, 1900 Jahre her) zum System der "epizyklischen Bewegungen" zur Erklärung der Himmelsbahnen der Planeten.

Es war Kopernikus (1473-1543), der die Idee des heliozentrischen Systems wieder aufgriff. Sein System erklärte auf einfache Art, weshalb Merkur und Venus nie weit von der Sonne entfernt zu sehen sind. Dabei ging er aber aus von Planeten auf Kreisbahnen und von festen "Planetensphären". Auch bei ihm war die Erdrotationsachse an einen festen Punkt in einer (weiten) Sphäre geknüpft. Damit konnten aber die Jahreszeiten nicht erklärt werden. Die Idee der festen Sphäre bestand nicht lange, da der "große Komet von 1577" die verschiedenen "Planetensphären" eindeutig durchdrang.

Basierend auf den sehr genauen Beobachtungen des dänischen Astronomen Tycho Brahe (1546-1610) konnte Kepler (1572-1630) das heliozentrische System perfektionieren, insbesondere indem er die Bahnen der Planeten leicht elliptisch ansetzte und der Rotationsachse der Erde eine feste Richtung gab.

Indirekt wurden die Argumente für die Drehung der Erde um die Sonne immer stärker, insbesondere auch mit einer Entdeckung 1610 durch Galilei (1564-1642) an Jupiter: der Planet Jupiter besitzt Monde die um Jupiter selber kreisen. Damit gab es ein eindeutiges Beispiel, dass nicht die Erde das einzige Zentrum aller Dinge ist, dass es also mindestens ein zweites Zentrum im Universum gibt. Desweiteren entdeckte Galilei Berge und Täler auf dem Mond sowie die Scheingestalten der Venus. Viele dieser Entdeckungen wurden von Kritikern Fehlern im neuen Galileischen Teleskop zugeschrieben oder sie wurden als Täuschungen abgetan!

Die Behauptung, die Erde drehe sich um die Sonne, alarmierte die Religionshüter in Rom. Zum einen wurde dadurch die Erde aus dem Zentrum des Universums entfernt, zum anderen stand auch die Theorie der Bewegung der Erde im Widerspruch zu einer Behauptung in der Bibel (Jozua), dass bei einer Schlacht "die Sonne stillstand", die Sonne also um die Erde kreist. Galilei wurde wegen der Behauptungen im Entwurf seines "Dialogo" verurteilt, landete im Gefängnis, und durfte nicht mehr publizieren. Später wurde die Gefängnisstrafe in Hausarrest in Arcetri (bei Florenz) umgewandelt. Dort schrieb er sein großes Werk ("Discorsi delle due nuove scienza"), in dem das geozentrische und heliozentrische Weltbild in Form einer Diskussion erörtert werden, ein Buch das mit der Aussage endet, dass vernünftige Leser selber entscheiden können. Das Buch wurde 1638 bei Elsevier in Leiden veröffentlicht, sofort vom Vatikan verboten mit dem unmittelbaren Erfolg einer weiten Verbreitung. Erst 1992 wurde Galilei von der Römischen Kirche rehabilitiert.

Zu beweisen, dass die Erde um ihre Achse rotiert, ist allerdings nicht einfach. So dachte man, dass dann alles was senkrecht hoch geworfen wird, etwas westlich davon herunterfallen würde. Zu der Zeit waren die Mechanik und ihre Gesetze noch nicht entwickelt! Experimente dazu waren allerdings auch viel zu ungenau, um irgend etwas erklären zu können.

Argumente dafür, dass die Erde rotiert, wurden verstärkt durch die Entdeckung 1665-66 von Cassini (1625-1712), Direktor des Observatoire de Paris, dass Jupiter und Mars selber rotieren. Dies waren aber immer noch Argumente aus Analogie, und daher keineswegs "Beweise".

Der große Beitrag Newtons (1643-1727) zu der Problematik ist, dass er die Mathematik weiter entwickelte, die für eine elegante Beschreibung der Bewegungen notwendig ist. Er postulierte, dass Materie durch eine Gravitationskraft angezogen wird. Diese Formulierungen erlaubten es, viele Phänomene einfach zu beschreiben.

Wechselwirkung von Rotation und Drehung

Noch ein Aspekt der Rotation der Erde muss erwähnt werden: die "Präzession". Schon in den griechischen Zeiten war bekannt, dass sich die Richtung der Erdrotationsachse ganz langsam ändert. Newton konnte dies mit seinen Gesetzen erklären. Die gegenseitige gravitative Wechselwirkung von Erde, Mond und Sonne liefert Drehkräfte, die zum Wackeln des rotierenden Erdspindels führen. Die Periode ist etwa 25700 Jahre. (Der Polarstern bleibt nicht "Polarstern"!) Newton sagte auch eine zusätzliche, kleinere Wackelei voraus, die "Nutation". Sie wurde 1748 von Bradley (1693-1762) aus Beobachtungen bestätigt. Die "Präzession" führt zu einer Verschiebung des "Frühlingspunktes" (Schnittpunkt des äquatorialen und ekliptischen Koordinatensystems am Himmel) und zur Wanderung dieses Punktes von jetzt im Sternbild Pisces (Fische) in den des Aquarius (Song "The age of Aquarius"!).

Mathematische Äquivalenz

Schliesslich kann noch angemerkt werden, dass das Sonnensystem mathematisch sowohl heliozentrisch als auch geozentrisch beschrieben werden kann und dass die Beschreibungen äquivalent sind. Um von der einen in die andere Beschreibung überzugehen erfordert es "nur" eine Koordinatentransformation. Allerdings ist die mathematische Formulierung des Systems als heliozentrisch sehr, sehr viel einfacher.

b. Die endgültigen Experimente

Das endgütige Experiment, das die Rotation der Erde um ihre Achse zeigte, gelang mit dem Pendel-Experiment von Foucault (1819-1868) in Paris. Ein Pendel schwingt eben mit einer festen Orientierung im Raum; die Erde bewegt sich darunter, mitsamt ihrer Drehung.

Das erste Pendel hing in Foucault's Wohnhaus (2 Meter Stahlkabel, daran eine 5 kg Kugel aus Kupfer). Da aber noch viel Kleinindustrie in Paris angesiedelt war und zu der Zeit Paris groß umgebaut wurde (Hausman und seine Boulevards), stellte er bald viele störende Einflüsse fest. Aragao (1786-1853), Direktor des Observatoire de Paris, erlaubte ihm nun, 1851 den 11 m hohen Meridianraum des Observatoire zu benutzen. Darin war beim Bau im Boden eine Nord-Süd-Linie angebracht. Das erste Kabel riss, und er musste die Aufhängung verbessern. Bald aber konnte er das Publikum zum Bestaunen der gegenüber der Meridianlinie sichtbar gemachten Erdrotation einladen.

2. Die Lichtgeschwindigkeit

Galilei hat wohl als erster versucht, die Lichtgeschwindigkeit zu messen. Zwei Laternen etwa eine Meile auseinander, seien abgedeckt. Ein Beobachter macht seine Lampe frei, der andere sieht dies und macht die seine frei. Die vergangene Zeit, in der der erste Beobachter die zweite Lampe sah war zwar sehr kurz, aber die vielen Unsicherheiten führten nicht zu einem sinnvollen Ergebnis.

Der Beweis, dass die Lichtgeschwindigkeit endlich ist, kam aus der Astronomie. Der Däne Ole Rømer (1644-1710), der seit 1672 bei Cassini am Observatoire de Paris arbeitete, sagte 1676 voraus, dass die Verfinsterung des inneren Jupitermondes durch Jupiter am 9. Nov. 1676 etwa 10 Minuten später auftreten würde als er aus dem Mittelwert der Zeitpunkte der vorherigen Verfinsterungen berechnet hatte. Die Erklärung lag in der Lichtlaufzeit zwischen Jupiter und Erde. Da eben die Erde und Jupiter sich während dieser Verfinsterung auf gegenüberliegenden Seiten der Sonne befinden, musste das Licht des Ereignisses einen größeren Teil des Erdbahndurchmessers überbrücken als durchschnittlich. Rømer hatte recht und berechnete, dass zum Überbrücken eines Erdbahndurchmessers das Licht etwa 22 Minuten braucht (dies entspricht einer Lichtgeschwindigkeit von etwa 220000 km/s).

Geometrie der Verfinsterung eines Jupitermondes. Je nach Position der Erde ist der Lichtweg zum Jupiter kürzer (HB) oder länger (HC), was zu einem Unterschied in der Lichtlaufzeit und damit zu einem Unterschied im Zeitpunkt des Sichtbarwerdens der Verfinsterung führt. A = Sonne, B,C,D,E Positionen der Erde, F=Jupiter, G,H=Jupitermond mit Verfinsterung.   Abbildung aus Simony (1990).

Damit war bewiesen, dass die Lichtgeschwindigkeit endlich ist. Halley (1656-1742) verbesserte die Berechnung erheblich (17 Minuten) an hand neuer Messungen.

Bei der vergeblichen Suche nach Sternen mit erkennbaren parallaktischen Bewegungen stellte Bradley 1728 fest, dass die Richtung zu den Sternen sich im Laufe des Jahres ändert (mit maximaler jährlicher Amplitude von 20 Bogensekunden!). Er erkannte die Analogie mit der Änderung der Richtung der Windfahne eines Schiffs bei Änderung seiner Fahrtrichtung. Aus seinem Bericht für die Royal Astronomical Society: "wenn zur Fortpflanzung des Lichts Zeit erforderlich ist, die scheinbare Lage eines ortsfesten Gegenstandes eine verschiedene sein muss, je nachdem ob sich das Auge [das Teleskop] in Ruhe befindet oder aber sich in irgendeine Richtung bewegt". Damit hatte er die "Aberration des Sternlichtes" entdeckt, ein Effekt, der die Endlichkeit der Lichtgeschwindigkeit untermauert.

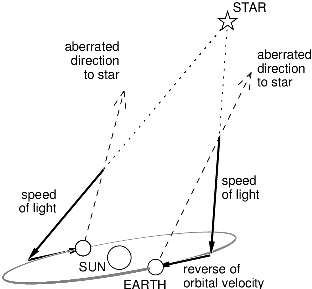Links: Geometrie einer Sternparallaxe. Rechts: Geometrie der Aberration. Durch die Bewegung der Erde sehen wir die Wellenfront des Lichtes unter einem Winkel gegenüber der wahren Richtung zum Stern. Daher erscheint die Richtung des Sterns bei endlicher Lichtgeschwindigkeit als Funktion der Geschwindigkeit des Betrachters.       Abbildungen aus Tobin (2003).

Die ersten gelungenen physikalischen Experimente zur Lichtgeschwindigkeit wurden unabhängig voneinander aber in Kenntnis der gegenseitigen Versuche von Foucault (1819-1868) und Fizeau (1819-1896) durchgeführt. Um 1850 stand das Problem der Lichtgeschwindigkeit und die Frage nach der Art des Lichtes (wellenartig oder korpuskular) im Mittelpunkt des Interesses, so auch bei Arago, Fizeau und Foucault in Paris.

Fizeau zielte auf die Bestimmung der Lichtgeschwindigkeit selber. Er entwarf ein Experiment, in dem Licht eines Heliostats zwischen die Zähne eines sich schnell-drehenden Rades zu einem entfernten Spiegel geschickt wurde, der das Licht reflektierte. Aus der Drehgeschwindigkeit zusammen mit der Sichtbarkeit des auch durch die Zähne rückkehrenden Strahls sollte auf die Geschwindigkeit des Lichts geschlossen werden können.

Foucault entwarf mit behilflichen Mechanikern ein komplexes Experiment, in dem Licht eines Sonnenteleskops zu einem entfernten, schnell-rotierenden Spiegel geschickt wurde, der das Licht reflektierte. Das Licht durchlief vor Ort Luft und der zweite Strahl vor Ort ein Rohr mit Wasser. Viele technische Schwierigkeiten mussten überwunden werden, so wie die mechanische Stabilität schnell-rotierender Spiegel, die genaue optische Ausrichtung, die Lichtmengen der beiden Strahlen im Okular, und vieles mehr, und er brauchte klares Wetter wegen der Lichtquelle, die Sonne.

Im "Wettbewerb" war Foucault erster und er konnte 1850 zeigen, dass die Geschwindigkeit des Lichts in Wasser kleiner ist als in der Luft. Damit war die Frage nach Wellen oder Korpuskeln beantwortet (Wellen!) und die Lichtgeschwindigkeit konnte aus den Messungen abgeleitet werden. Er wiederholte 1862 das Fizeausche Experiment in neuer (und kleinerer) Fassung und bestimmte die Lichtgeschwindigkeit zu 298000 km/s, ein Wert, der nur 1.5% vom heutigen abweicht.

3. Entfernung Erde-Sonne

Die Bestimmung der Entfernungen im Sonnensystem ist mit der Bestimmung der Lichtgeschwindigkeit verknüpft. Hat man eine Entfernung geometrisch bestimmt, so kann die Lichtgeschwindigkeit berechnet werden, und umgekehrt. Rømer hatte eben aus den Verfinsterungen des inneren Jupitermondes zur Relation zwischen Lichtgeschwindigkeit und Geometrie des Sonnensystems wichtige Fakten geliefert. Um so wichtiger sind unabhängige geometrische Bestimmungen der Entfernungen.

Schon 1716 hatte Halley der Royal Astronomical Society eine Methode vorgestellt, um beim Venus-Transit von 1761 eine geometrische Bestimmung im Planetensystem vorzunehmen. Viele Expeditionen reisten von Europa aus in die Welt, um die Transite (sie treten immer in Pärchen auf) von 1761 und 1769 zu vermessen. Davon ist die von James Cook (1728-1779), der den Transit in Tahiti beobachtete, die bekannteste. Aus den vielen allerdings nicht sehr genauen Messungen, die auch wegen der noch ungenauen geografischen Längenbestimmungen weitere Unsicherheiten in die Berechnungen hineinbrachten, leitete schliesslich Encke (1791-1865) in Berlin die "Sonnenparallaxe" ab, die für die AE zu einem Wert führte, der nur 10% vom heutigen abweicht.

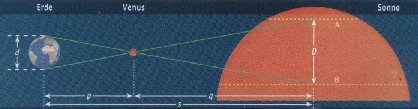Geometrie eines Venus-Transits, aus der man (bei bekanntem Erddiameter) die Entfernung Erde-Sonne ableiten kann. Die Venus bewegt sich vor der Sonne entlang, von Nord- und Süpol der Erde aus gesehen entlang Bahn B beziehungsweise A.   Abbildung aus Neumann (2004).

Ein genauerer Wert folgte schliesslich aus der Lichtgeschwindigkeit zusammen mit den Zeitpunkten der Verfinsterungen der Jupitermonde. Le Verrier (1811-1877), Direktor des Observatoire de Paris, leitete 1853 einen genauen Wert aus den allgemeinen Bewegungsverhältnissen im Sonnensystem zusammen mit den Newtonschen Gesetzen ab. Dafür waren Gleichungen mit mehr als 500 Gliedern, um alle gegenseitigen Wechselwirkungen im Sonnensystem zu berücksichtigen, notwendig. (Aus Merkwürdigkeiten der Bahn des Planeten Uran hatte Le Verrier 1846 mit Hilfe dieser Gleichungen die Existenz eines weiteren Planeten vorausgesagt; Neptun wurde bald danach an der berechneten Position entdeckt!)

Die Bedeutung der Größe der AE liegt auch darin, dass es erst damit und mit Hilfe der Newtonschen Gesetze zu der Berechnung von Massen von Objekten im Sonnensystem kommen kann, und damit zu der Masse eines ganz wichtigen Sterns: der Sonne.