Probleme in und mit der Kosmologie?

    Klaas S. de Boer
    Argelander Institut für Astronomie (Abt. Sternwarte), Univ. Bonn

Seit Albert Einstein seine spezielle (1905) und dann die allgemeine Relativitätstheorie (1915) formulierte, haben Forscher an der mathematischen Beschreibung getüftelt. Damals schien das Universum statisch bzw. stationär: der Weltraum war leer außer den vielen bekannten Galaxien mit ihren Sternen und leuchtenden Gaswolken. Befriedigend war dies nicht, da die ewig wirkende Gravitation alles aufeinander zukommen lassen sollte. Daher schuf Einstein in seinen Gleichungen einen extra Parameter, die sogenannte kosmologische Konstante, Λ ("Lambda"), die gewissermaßen der Gesamtgravitation des Universums entgegenwirkte. Später hat Einstein diesen Faktor wieder herausgenommen, wobei er gesagt haben soll, Λ sei seine größte Eselei ("Blunder") gewesen.

Einsteins Relativitätstheorie und die darin enthaltene Beschreibung der Gravitation hat sich bewährt. Alle irdischen Phänomene wurden selbstverständlich richtig erfasst und ebenfalls die sehr großen Schwerkräfte bei Neutronensternen und Schwarzen Löchern, wie rezent bei der Vermessung der Gravitationswellen dokumentiert wurde. Alle Forscher haben daher angenommen, dass die Beschreibung der Schwerkraft für Bedingungen, wo sie ganz klein ist, ebenfalls von der Relativitätstheorie erfasst werden. Letzteres muss aber noch unter Beweis gestellt werden....

Das Verhalten des Universums

Erste Indizien für die Tatsache, dass weiter entfernte Galaxien sich von uns weg bewegen, kamen von Carl Wirtz (damals in Strasbourg). Diese Tatsache wurde 1927 von Lemaître in Leuven als eine Expansion des Raumes gedeutet, und das Universum sei in seinen Anfängen sehr klein gewesen. Hubble am Palomar Observatorium hat dann mit mehr Daten den Befund der Expansion untermauern können. Die frühe Geschichte der Entdeckung der Expansion wurde von Geffert (2017) zusammengefasst.

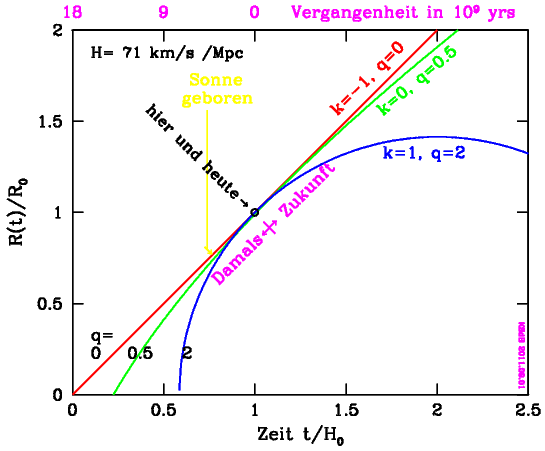
Nun zum Verhalten des Universums über lange Zeiten. Unter der Annahme, das Universum sei auf größten Skalen homogen, führen die Gleichungen zu relativ einfachen Lösungen, die grafisch dargestellt werden können. Eine Lösung heißt die "kritische", da sie eine euklidische Geometrie (die uns allen bekannte Geometrie) und genau die richtige Materiedichte (die "kritische") hat. Diese Lösung wird (auch aus ästhetischen Gründen) favorisiert. In der Grafik ist es Fall C und das Universum sei dann 13.8 Gyr (Gyr= eine Miliarde Jahre) alt. Die Parameterwerte dieses Modell sind k=0 und q=0.5. Der Parameter k steht für die Art der Geometrie: k=0 ist euklidisch, k=−1 ist die "hyperbolische" (mit q zwischen 0 und 0.5), k=+1 die "sphärische Geometrie" (mit q größer als 0.5). Jede Kombination der Parameterwerte führt zu einem anderen Verhalten des Universums. q vertritt die Art der Bremsung.

Das Diagramm zeigt Zeit t gegen Größe R(t), mit dem Punkt "hier und heute". Drei spezielle Möglichkeiten für das Verhalten sind eingezeichnet (mit Werten von k und q): Fall E (immer weiter expandierend), Fall C (Grenzfall), und Fall R (später kontrahierend). Alles dazwischen ist ebenfalls möglich. Fall C ist das Modell, das ewig expandiert aber allmählich verlangsamt, ohne zum Stillstand zu kommen. In just diesem Modell ist das Universum 13.8 Gyr alt. Dies ist in der Grafik in Richtung "Damals" abzulesen aus dem Schnittpunkt der Linie des Modells (grün) mit der Zeitachse (die "Zurückschauzeit" ist am oberen Rand in Gyr angegeben). Die Sonne entstand vor 4.5 Gyr.

Expansionsrate des Universums und H₀
Die Expansionsrate des Universums wurde anfänglich von Hubble (1929) bestimmt. Nach Verbesserung der Eichung des hierzu wichtigen Typs der variablen Sterne, der Cepheiden (siehe Entfernungsbestimmung), haben sich viele mit der Neubestimmung der Expansionsrate beschäftigt. Um diese Expansionsrate, dann Hubble Konstante H₀ genannt, wurde heftigst gestritten, da die von unterschiedlichen Gruppen favorisierten zwei Werte (50 und 100 km/s /Mpc) anscheinend nicht in Einklang zu bringen waren.

Probleme mit den Werten der Hubble Konstante

Der stellare Hubble Konstante
Das Hubble Teleskop (HST) ermöglichte es, die so nützlichen Cepheiden in weiter entfernten Galaxien zu entdecken, um so die Expansionsrate besser bestimmen zu können (auch wegen dieser Aufgabe wurde das HST nach Hubble benannt). Die Konstante wurde dann einvernehmlich zu 71 km/s /Mpc bestimmt. Die später verstandenen Supernovae des Typs Ia, die gelegentlich aufflammen, auch in weit entlegenen Galaxien, ermöglichten es, die Expansionsrate über viel größere Entfernungen auszuloten.

Die Erforschungen aller Eichschritte in der Sequenz Parallaxe−Cepheiden−SN Ia gingen

Hubble Konstante H0 und wie ihr Wert im Laufe der Jahre durch Neueichungen angepasst wurde (nach Freedman, 2017; New Scientist Dec. 2018; Ergänzung 2019). Blau: H0 aus stellaren Bestimmungen. Rot: H0 aus CMB und Standardmodell.

immer weiter und die Bestimmung dieser "stellaren Hubble Konstante" wurde immer genauer. Der neueste Wert von H₀ liegt (Riess+ 2019) bei 74.2 km/s /Mpc (siehe Abbildung). Inzwischen gibt es ein Problem, da der aus der CMB bestimmte Wert inzwischen stark abweicht.

Urknall Strahlung (CMB) und H₀
Im Jahre 1964 wurde die "kosmische Hintergrundstrahlung" (per Zufall) als restliches Rauschen in Radiosignalen vom Himmel entdeckt. Aus allen Himmelsrichtungen kommt diese Strahlung, die effektiv eine Strahlungstemperatur von etwa 2.7 Grad Kelvin hat. Sie wurde als ein Überbleibsel der ganz heißen Strahlung aus der Zeit des Urknalls gedeutet.
Das Maximum der Strahlung liegt bei etwa 1.5 mm Wellenlänge. Um diese Strahlung genau zu untersuchen, waren Messungen aus dem Raum notwendig. Mehrere Satelliten sind gebaut worden (COBE, WMAP, Planck), um die kosmische Hintergrundstrahlung (Cosmic Microwave Background, CMB) immer genauer zu vermessen (siehe CMB Resultate). Die winzigen räumlichen Inhomogenitäten in dieser Strahlung führten zusammen mit Modellen für das Verhalten des Universums zu Werten für viele der Modellparameter.

Die Werte von H₀ sowie die Unsicherheit in der Bestimmung wurden im Laufe der Jahre mit den weiterführenden Anpassungen des Standardmodells immer kleiner. Der beste Wert aus CMB und Standardmodell ist z.Z. H₀ = 66.5 km/s /Mpc (Abbildung). Es gibt eindeutig kein Überlappen des Unsicherheitsbereichs mit dem der stellar bestimmten Hubble Konstante.

Wo steckt das Problem? Steinmetz (2019) diskutiert einige Möglichkeiten mit "neuer" Physik, wie relativistische Teilchen, wechselwirkende Dunkle Materie, oder zeitlich veränderliche Dunkle Energie und Raumkrümmung. Aber das alles überbrückt die Diskrepanz nicht.

Anmerkungen zu Problemen mit dem "Standardmodell"

Dunkle Materie
In den 1970er Jahren wurde entdeckt, dass bei mancher Galaxie die Außenbezirke eine deutlich größere Umlaufgeschwindigkeit um das jeweilige Galaxien-Zentrum aufweisen als aus der gravitativen Wirkung der Materie der Galaxie hervorgehen konnte (Rubin & Ford 1970, Carnegie Institut, USA; Bosma 1981, Groningen, NL). Schon in den 1930er Jahren hatte Zwicky aus seiner Studie der Geschwindigkeiten der Galaxien in einem Galaxienhaufen abgeleitet, dass der ganze Haufen viel mehr an Masse haben muss, als aus den bekannten Daten dokumentiert werden konnte.

Theoretische Modelle zur Rotation der Galaxien schienen im Einklang mit den Daten gebracht werden zu können, wenn man mehr Schwerkraft oder eigentlich mehr Materie annahm, als Astronomen dokumentieren konnten. Dabei ging es um Faktoren im Bereich von 10! Diese große Menge an zusätzlicher Materie war nicht sichtbar, wurde alsbald Dunkle Materie genannt (siehe de Boer 2017: Woher kommt der Begriff "Dunkle Materie"?).

Dunkle Materie ist eine hypothetische Materie, die bisher NUR für zusätzliche Schwerkraft sorgt, um die Modellierung der Geschwindigkeit der Rotation einer Galaxie passend zu den Messdaten zu machen. Und sonst nichts.

Inzwischen wurde dieses Verhalten der Umlaufgeschwindigkeit bei unzähligen Galaxien nachgewiesen. Allerdings hatte Bosma schon gemerkt, dass in der Modellierung seiner Galaxien mit Dunkler Materie die räumliche Verteilung der eingesetzten Dunklen Materie der Verteilung bekannter Materie sehr ähnelte. War das bedeutsam?

Die Bestimmung der Menge an Dunklen Materie, die zur Erklärung der Geschwindigkeiten der Galaxien in einem Galaxienhaufen notwendig erscheint, ist ebenfalls problematisch. Die Gesamtmenge der Materie wird abgeleitet mithilfe des sogenannten Virialtheorems. Von den 4 Bedingungen, die bei dieser Anwendung erfüllt sein müssen, ist die wichtigste, dass das Haufensystem im Gleichgewicht sein soll. Nun fehlt zur Erreichung eines Gleichgewichts vermutlich kosmologisch gesehen die Zeit. Auch sind die Galaxienhaufen i.a. schlecht im Umfeld definierbar. Daher ist nicht gesichert, dass die Galaxienhaufen sphärisch sind, was alleine schon die Vorbedingung des Gleichgewichts verletzt.

Mordechai Milgrom (Weizmann Institit, Israel) hat den ersten Ansatz gemacht, das Newtonsche Gravitationsgesetz anzupassen. Ohne irgendwelche "herbeigezauberte Materie" fand er 1983 eine Formulierung, womit in der Tat die Geschwindigkeiten am Rande der Galaxien groß bleiben. Seine Theorie heisst MOND (modifizierte Newtonsche Dynamik). Inzwischen wurde MOND auf vielen Galaxien verschiedensten Typs angewendet und stets waren mit MOND die gemessenen Geschwindigkeiten und andere Eigenschaften ohne Bedarf an hypothetischer Materie erklärbar. Ein Erfolg.

Das Problem der für Galaxienhaufen abgeleiteten großen Menge an DM scheint auch nicht mehr groß zu sein. Bob Sanders am Kapteyn Institut in Groningen, NL, der sehr intensiv bezüglich Fragen zu MOND und DM geforscht hat, zeigte 2003, dass bei Anwendung von MOND kaum noch Materie fehlt.

Die Teilchenphysik liefert auch keine Abhilfe. Es gibt keinen einzigen Hinweis auf die Existenz irgendeiner Materie, die als Eigenschaft (nahezu nur) Gravitation hat. Teilchenphysiker haben mit viel Phantasie ihre Modelle der Elementarteilchen nach Möglichkeiten für weitere und sonderbare Teilchen mit exotischen Namen (WIMPS, Axionen, sterile Neutrinos, Monopole, ....) ausgelotet. Das hat bisher nicht gefruchtet. Des weiteren haben Experimentalphysiker in und mit Teilchenbeschleunigern auch nach sonderbaren Teilchen gesucht, in der Hoffnung etwas zu finden, das zu den Eigenschaften der hypothetischen Dunklen Materie passt. Dies war, genau wie bei den Theoretikern, erfolglos.

Es gibt hier nur eine Schlussfolgerung: wegen der immer noch (und nur) hypothetischen Natur der DM muss eine andere Lösung für das Masse/Schwerkraft Problem herbeigeführt werden. Man komme nicht mehr darum herum anzuerkennen, dass das Newtonsche Gravitationsgesetz unter den Bedingungen sehr geringer Kräfte offenbar nicht zutrifft. Es muss ersetzt werden, und da bietet MOND eine gute Lösung.

DM oder MOND?   Sowohl mit der Hypothese DM als mit der Hypothese MOND können selbstverständlich die gemessenen "Probleme" bei den Geschwindigkeiten in Galaxien "erklärt" werden. Dabei ist DM seit langem nichts mehr als eine Hypothese. MOND bringt eine Anpassung des Gravitationsgesetzes, wobei es im neuen Gesetz einen freien Parameter gibt. Dieser Parameter ist genau so "frei" wie, z.B., die Newtonsche Gravitationskonstante oder die Konstante der Lichtgeschwindigkeit. In allen drei physikalischen Gesetzen wurde der Wert der Konstante aus Messungen abgeleitet.

Homogenität des Universums
Die mathematischen Gleichungen, die die Struktur des Universums beschreiben sollen, sind von einer verführerischen Einfachkeit. Dafür musste allerdings eine ganz wichtige Annahme gemacht werden und zwar die der Homogenität des Universums. Ohne diese Annahme müsste jedes Modell jede lokale Verdichtung der Materie (wie die einer jeden Galaxie) wie grob auch immer separat berücksichtigen.
Stellt man sich den Urknall als Explosion vor, so ist es undenkbar, dass das alles zu einem sich homogen ausbreitenden Materiegetümmel werden würde. Die CMB strahlt aber ungemein homogen am Himmel. Wenn sich das Universum nach dem Urknall

Eine extrem schnelle Expansion (Inflation) wurde für das frühe Universum postuliert, um in den Modellen die großskalige Homogenität der kosmischen Hintergrundstrahlung zu bewirken (siehe oben). Man hat die Phase der Inflation nicht mit sinnvoller Physik herbeiführen können. Sie wird den Modellen einfach auferlegt, liefert dann Resultate, die weitgehend mit dem CMB im Einklang sind.

rasant schnell expandiert hätte, derart schnell, dass kleine anfängliche Inhomogenitäten keine Chance gehabt hätten sich zu entwickeln, besser noch, dass sie durch eine rasante Expansion geglättet worden wären, dann wäre alles danach homogen gewesen. Guth und Tye haben 1980 zur Lösung dieses Homogenitätsproblems eine Inflationsphase vorgeschlagen.

Mehrere Versuche wurden unternommen, das Problem der Homogenität anzugehen. Da die Inflation im Standardmodell mit seinen vielen frei wählbaren Parametern eingebettet ist, hängt darin alles mit allem zusammen. Über die Inflation wird wohl noch viele Jahre diskutiert und geforscht werden.

Entfernungen der Galaxien in einem Streifen entlang dem Himmelsequator. Die "Karte" zeigt die räumliche Verteilung (bis Entfernung z=0.15). Die Galaxien sind nicht homogen verteilt, das Universum kann nicht als homogen angesehen werden. (Bild SDSS)

Aber, das Universum ist nicht homogen ! Im 20. Jht wurden in vielen Himmelsrichtungen Galaxien "gezählt". Es ging um die Bestimmung der räumlichen Verteilung der Galaxien. Bald wurde klar, dass es im Universum große Gebiete ohne Galaxien gibt. Diese Gebiete wurden voids (etwa Leerräume) genannt. Die gezeigte Abbildung ist das Ergebnis vieler Jahre Arbeit im Sloan Digital Sky Survey (SDSS).
Ist die Inhomogenität im Universum von Bedeutung für die Einsteinschen Gleichungen, die die Homogenität voraussetzen? Vielleicht nicht, aber in anderen Bereichen könnte es schon ein Problem sein.

Dunkle Energie
Untersuchungen von Perlmutter+ (1999) an neu entdeckten weit entfernten SN Ia zeigten, dass die Beziehung zwischen Entfernung und Geschwindigkeit (sprich: die Hubble Relation) nicht mehr so ganz gerade war. Bei gemessener Rotverschiebung schienen die SN Ia heller als bei der aus dem Licht der Galaxie gemessenen Rotverschiebung erwartet. Dies kann man unter Beibehaltung der intrinsischen Helligkeit dieser Supernovae erklären,

Dunkle Energie ist eine hypothetische Kraft, die das Universum jetzt schneller auseinander treibt als in der Vergangenheit. Damit wird das Modell der Expansion des Universums derart angepasst, dass die Geschwindigkeit der Galaxien zu den Daten der SN Ia passen.

wenn das Universum jetzt schneller expandiert als in der Vergangenheit (Objekte bei größerer Rotverschiebung, wie die fernen SN Ia, sieht man eben weit in der Vergangenheit). H₀ sei damals kleiner als heute.

Wenn die Expansion in der Vergangenheit langsamer war, sollte ein Etwas die Expansion beschleunigen. Da kein bekannter Mechanismus vorhanden war, postulierte man die "Dunkle Energie", die eben die Beschleunigung bewirken sollte. Damit war das Problem gelöst, allerdings auf gleiche Art wie bei der Dunklen Materie, durch etwas Hypothetisches, ohne physikalischen Prozess.

Dunkle Energie oder ein nicht-homogenes Universum?
Es gibt mehrere Gründe, die Hypothese zur Dunklen Energie in Frage zu stellen.
- Zum einen ist ungesichert, dass alle SN Ia sich identisch benehmen. Wenn, z.B. der Stern, der wegen der vom Nachbarn angesammelten Materie explodieren würde, relativ schnell rotiert, so kann er mehr an angesammelter Masse tragen als ohne Rotation; damit würde er schwerer werden können als die sonst gut definierten 1.4 Sonnenmassen und dadurch wäre die Supernova Explosion auch heller.
- Zweitens, für viele der Galaxien mit einer SN Ia wurde die Rotverschiebung nicht aus Spektren, sondern aus Photometrie abgeleitet, was sehr ungenau ist.
- Drittens, das Postulat der Dunkle Energie beinhaltet eine Verletzung des Gesetzes zur Erhalt von Energie. Woher soll die Energie kommen, die die Expansion beschleunigte?
- Ein ganz andersartiges Problem wurde von David Wiltshire (2007; Dam+ 2017) in Christchurch, NZ, gesehen. Er hat Modelle für ein nicht homogenes Universum erprobt.

Homogenität oder Nicht? Es gibt eine nette Parallele zu der beim freien Fall von F. Baumgartner in 2012 erreichten Überschallgeschwindigkeit. Er sprang in einem Raumanzug aus 39 km Höhe. Die Erwartung aus der Physik fallender (glatter) Körper war: es wird maximal die Schallgeschwindigkeit erreicht. Eine neue Modellierung eines frei-fallenden Körpers mit nicht-homogener Oberfläche (Helm, Arme, Beine, Kameras) erlaubte sehr wohl eine Überschallgeschwindigkeit. Kein Bedarf für einen Sonderantrieb! Siehe Guerster & Walter (2017): "Freier Fall mit Überschall".

In ihnen wäre die Expansionsrate in den Voids größer als in der Nähe von Galaxienhaufen. Der Mittelwert dieser unterschiedlichen Raten über längeren Blickrichtungen würde zu einem kleineren H₀ führen. Er sieht daher keinen Bedarf für Dunkle Energie! Kein Sonderantrieb, das nicht-homogen sein bewirkt eine gleichbleibende Hubble Konstante H₀.

Anordnung der Zwerggalaxien
Mit dem Standardmodell der Kosmologie wurden Berechnungen über Strukturbildung im Universum für die Zeit nach dem Urknall gemacht. Angenommen wurde eine ordentliche Menge an Dunkler Materie, die sich in kleine Dichtefluktuationen weiter verdichten sollte, um mit diesen gravitativen Zentren dann "normale" Materie hineinziehen zu können. Damit sollten sich kleine Galaxien bilden, mit Sternentstehung und all dem, was zu einer Galaxie gehört.

Das Objekt NGC 2623 zeigt zwei kollidierende Galaxien. Die Gezeitenreibung bewirkt, dass Materieschweifen herausgezogen werden, in den sich Sterne bilden.  Diese Schweife haben eine Orientierung und Umlaufrichtung, die auf die Bahnbewegung der beiden Galaxien zurückgeht.  Reste der Schweife bilden später eine Scheibe mit Zwerggalaxien.   Im Hintergrund sieht man weit entlegene Galaxien. (Bild: NASA, ESA, Hubble.)

Da das Universum als homogen vorausgesetzt wurde, sollten auch die kleinen Galaxien mehr oder weniger gleichmäßig verteilt sein. Dennoch würden viele kleine Galaxien einander begegnen, in ihren gegenseitigen (gravitativen) "Potentialtopf" geraten und verschmelzen, auf diese Art zu immer größeren Galaxien wachsend.

Ein Ergebnis dieser Strukturbildungs-Modelle ist, dass um große Galaxien noch viele Zwerggalaxien gleichmäßig verteilt (sprich: sphärisch) vorhanden sein sollten. Bei unserer Galaxis ist dies nicht so; es gibt Zwerggalaxien, aber die sind eher scheibenartig um die Milchstraße angeordnet (Metz & Kroupa 2007; Bonn). Alsbald sprachen die Modell-Theoretiker vom "Problem der fehlenden Zwerggalaxien", implizit eine gewisse "Bringschuld" den beobachtenden Astronomen auferlegend. Daraufhin wurden doch noch einige kleine nahe Galaxien entdeckt; sie lagen aber auch in dieser Scheibe! Dann stellten Forscher fest, dass die Andromeda Galaxie, unser nächster Nachbar, ebenfalls keine homogene "Wolke" an Zwerggalaxien besitzt. Dazu kam, dass in numerischen kinematischen Simulationen von wechselwirkenden Galaxien eindeutig die vorhandenen (und durch Gezeitenkräfte hervorgerufenen) Materieströmungen nachgebildet werden konnten.

Die Galaxie Cantaurus A (NGC 5128) ist von vielen Zwerggalaxien umgeben (auf der Skala dieses Bildes nicht zu erkennen), die offenbar in einer Scheibe angeordnet sind (Bild: MPG, ESO).

In ihnen bildeten sich Sterne und sogar Zwerggalaxien. Sie können u.U. die Hauptgalaxie umkreisen in einer Richtung entgegen der Rotationsrichtung der Hauptgalaxie (Pawlowski+ 2011; Bonn). Unabhängig vom komplizierten Standardmodell konnten auf direktem, kinematischem Weg in einer Scheibe gelegene Zwerggalaxien entstehen.

Inzwischen wurde für die Galaxie "Centaurus A" in einer weit entfernten Galaxiengruppe festgestellt, dass ihre Begleitgalaxien auch in einer Scheibe angeordnet sind (Müller+ 2018).
Da es nun mehrere Beispiele für eine nicht sphärische Anordnung gibt, muss erneut eine der Vorhersagen des sogenannten Standardmodells als "nicht mit der Realität im Einklang" eingestuft werden.

Quasare
Ein Quasar hat in seinem Zentrum ein gewaltiges Schwarzes Loch und ist umgeben von einer sogenannten Akkretionsscheibe. Quasare strahlen Unmengen an Licht ab, sie können daher bis in sehr große Entfernungen gesehen werden. Ende 2017 wurde über die Entdeckung eines rekordverdächtigen Quasars berichtet (siehe Quasar J1342+0928), ein Quasar in einer Entfernung gleich einer Rückschauzeit von 13.1 Gyr.

Die Entfernung folgte aus der Rotverschiebung von spektralen Merkmalen. Eine derartige Entfernung bedeutet, dass der Quasar in weniger als 600 Millionen Jahren nach dem Urknall komplett etabliert gewesen sein muss. Reichen die 600 Millionen Jahre dafür? Oder soll das Universum älter sein als 13.8 Gyr? Diese Fragen müssen noch beantwortet werden. Unter Umständen ist das Standardmodell auch hier nicht mehr passend....

Zusammenfassend:
Das sogenannte "Standardmodell" der Kosmologie enthält eine große Zahl an Annahmen. Daher ist es möglich, eine Vielzahl verschiedener Verhaltensweisen des Universums an die Messungen anzupassen. Mehrere Forschergruppen haben sich mit Problemen des Standardmodells auseinandergesetzt und in verschiedenen Bereichen alternative Lösungen ohne exotische Physik vorgestellt. Es ist nur eine Frage der Zeit, bis auch die Mehrzahl der Forscher die Notwendigkeit einer fundamentalen Anpassung des Standardmodells einsieht.

Um den gedanklichen Zugang zu den oben geschilderten Fragen zu erleichtern, sind die besprochenen Probleme vereinfacht wiedergegeben.
Bei der Vorbereitung dieses Textes wurden die unten angegebenen Quellen und verschiedene Seiten in Wikipedia benutzt. Die sehr gediegene, umfassende Arbeit von Kroupa (2012) ist hervorzuheben.

 
Quellen:
Beyvers, G., Krusch, E.   2007, "Kleines 1×1 der Relativitätstheorie", ISBN 978-3-8334-6291-7
Bosma, A.   1981, Astronom. Journal, 86, 1791
Dam, L.H., Heinesen, A., Wiltshire, D.L.   2017, Month. Not. Roy. Astr. Soc., 472, 835
de Boer, K.S.   2017, in Astronomie+Raumfahrt, 54, S.6
Freedman, W.   2017, Nature Astronomy, 1.10169
Geffert, M.   2017, in Astronomie+Raumfahrt, 54, S.16
Guerster, M., Walter, U.   2017, PLos ONE, 10.1371/journal.pone.0187798
Guth, A. H., Tye, S.-H. H.   1980, Physical Review Letters, 44, 631
Hubble, E.   1929, Proc. Nat. Acad. Sciences, 15, p.168-173
Kroupa, P., Famaey, B., de Boer, K.S., et al.   2010, Astron. & Astrophys. 523, A32
Kroupa, P.   2012, "The dark matter crisis: falsification of the current standard model of cosmology",
    Publ. Astron. Soc. Australia, 4, p.395-433
Metz, M., Kroupa, P.   2007, Month. Not. Roy. Astron. Soc., 376, 387
Milgrom, M.   1983, Astrophys. Journal, 270, 371
Müller, O., Pawlowski, M., Jerjen, H., Lelli, F.   2018, Science 359, p.534-537
Pawlowski, M.S., Kroupa, P., de Boer, K.S.   2011, Astron. & Astrophys. 532, A118
Pawlowski, M.S., Famaey, B., et al.   2014, Month. Not. Roy. Astron. Soc., 442, 2362
Perlmutter, S., et al.   1999, Astrophys. Journal, 517, 565
Riess, A.G. et al.   2019, arxiv:1903.07603;   auch Riess, A.G., et al., 2016, Astrophys. Journal, 826, 56, 31
Rubin, V. C., Ford, W. K. Jr.   1970, Astrphys. Journal, 159, 379
Sanders. R.H.   2003, Month. Not. Roy. Astr. Soc. 342, 901
Steinmetz, M.   2019, Physik Journal (DPG), 18, 16
Wiltshire, D.L.   2007, "Exact Solution to the Averaging Problem in Cosmology". Physical Review Letters, 99, 25

(2019.06.09)   erste Version 2018.02.04   kosmoproblem.html