8.13 Point(BoaMapping.Map):

Point(BoaMapping.Map): $<$ BoaPointing.py

    NAM: Point (class)
    DES: An object of this class is responsible for the reduction of
         pointing scan(s)

History:

NAM: BoaPoint.py (module)
DES: contains the BoA Pointing reduction tools

Additional information:



Example: In the figures below the graphical output of a pointing of a single scan (8.1) and of accumulated scans (8.2) is shown.

Figure 8.1: Graphical output of a pointing of a single scan of a point source, colors represent different scans, symbols are measured values, drawn lines are Levenberg-Marquardt fits.

Figure 8.2: Graphical output of a pointing of accumulated scans of a point source, colors represent different scans, symbols are measured values, drawn lines are Levenberg-Marquardt fits.

Levenberg-Marquardt:

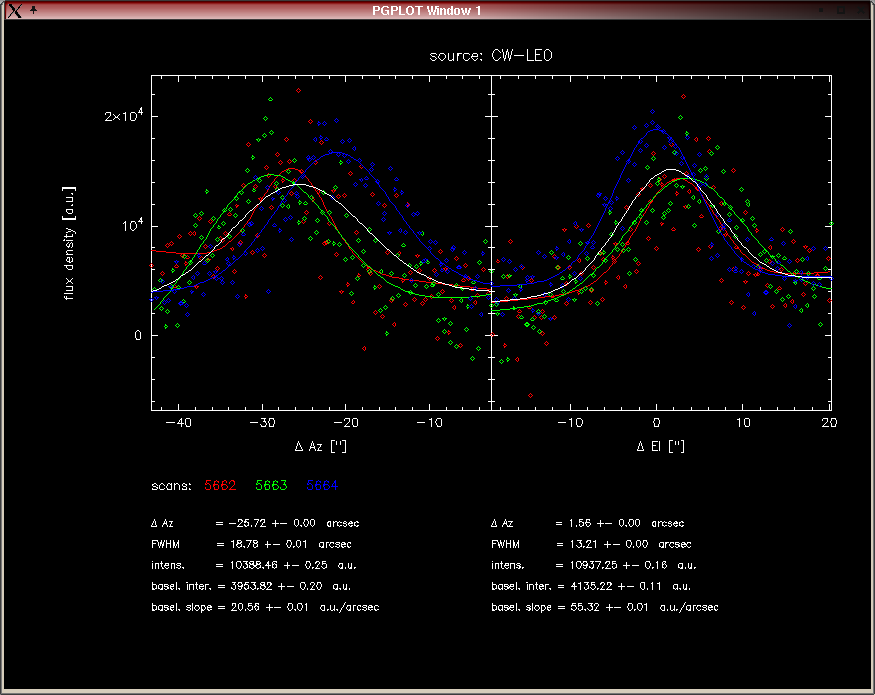
The Levenberg-Marquardt algorithm can be thought of as a trust-region modification of the Gauss-Newton algorithm. Levenberg-Marquardt steps $s_{k}$ are obtained by solving subproblems of the form

$${\rm min} \, \left\{ \frac{1}{2} \left\Vert f^{'}(x_{k})s ... ...{2}_{2}: \Vert D_{k^{s}} \Vert _{2} \le \Delta_{k} \right\}$$ (8.1)

for some $\Delta_{k} > 0$ and scaling matrix $\Delta_{k}$. The trust-region radius is adjusted between iterations according to the agreement between predicted and actual reduction in the objective function. For a step to be accepted, the ratio

$$\rho_{k} = \frac{r(x_{k}) - r(x_{k} + s_{k})} {r(x_{k}) - ... ...\right\Vert^{2}_{2}: \left\Vert D_{k^{s}} \right\Vert _{2}}$$ (8.2)

must exceed a small positive number.(typically .0001). If this test is failed, the trust region is decreased and the step is recalculated. When the ratio is close to one, the trust region for the next iteration is expanded.

Levenberg-Marquardt codes usually determine the step by noting that the solution of 8.1 also satisfies the equation

$$\left( f^{'}(x_{k})^{T}\,f^{'}(x_{k}) + \lambda_{k}\,D^{T}_{k}\,D_{k} \right)\,s_{k} = -f^{'}(x_{k})^{T}\,f^{'}(x_{k})$$ (8.3)

for some $\lambda_{k} \ge 0$.

The Lagrange multiplier $\lambda_{k}$ is zero if the minimum-norm Gauss-Newton step is smaller than $\Delta_{k}$; otherwise $\lambda_{k}$ is chosen so that $\Vert \Delta_{k}\,s_{k} \Vert _{2} = \Delta_{k}$ .

Equations 8.3 are simply the normal equations for the least squares problem

$${\rm min} \left\{ \left\Vert \left[ \begin{array}{c} f^{... ... \right] \right\Vert^{2}_{2}: s \in \mathbb{R}^{n} \right\}$$ (8.4)

Efficient factorization of the coefficient matrix in 8.4 can be performed by a combination of Householder and Givens transformations. The Levenberg-Marquardt algorithm has proved to be an effective and popular way to solve nonlinear least squares problems.